
【题目】已知平面向量![]() ,
,![]() ,
,![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 的最大值是______.
的最大值是______.
【答案】3![]()
【解析】
分别以![]() 所在的直线为x,y轴建立直角坐标系,分类讨论:当{|
所在的直线为x,y轴建立直角坐标系,分类讨论:当{|![]() |,|
|,|![]() |}={1,2},|
|}={1,2},|![]() |=3,设
|=3,设![]() ,则x2+y2=9,则
,则x2+y2=9,则![]() (1+x,2+y),有|
(1+x,2+y),有|![]() |
|![]() 的最大值,其几何意义是圆x2+y2=9上点(x,y)与定点(﹣1,﹣2)的距离的最大值;其他情况同理,然后求出各种情况的最大值进行比较即可.
的最大值,其几何意义是圆x2+y2=9上点(x,y)与定点(﹣1,﹣2)的距离的最大值;其他情况同理,然后求出各种情况的最大值进行比较即可.
分别以![]() 所在的直线为x,y轴建立直角坐标系,
所在的直线为x,y轴建立直角坐标系,
①当{|![]() |,|
|,|![]() |}={1,2},|
|}={1,2},|![]() |=3,则
|=3,则![]() ,
,
设![]() ,则x2+y2=9,
,则x2+y2=9,
∴![]() (1+x,2+y),
(1+x,2+y),
∴|![]() |
|![]() 的最大值,其几何意义是圆x2+y2=9上点(x,y)与定点(﹣1,﹣2)的距离的最大值为
的最大值,其几何意义是圆x2+y2=9上点(x,y)与定点(﹣1,﹣2)的距离的最大值为![]() 3
3![]() ;
;
②当{|![]() |,|
|,|![]() |}={1,3},|
|}={1,3},|![]() |=2,则
|=2,则![]() ,x2+y2=4,
,x2+y2=4,
∴![]() (1+x,3+y)
(1+x,3+y)
∴|![]() |
|![]() 的最大值,其几何意义是圆x2+y2=4上点(x,y)与定点(﹣1,﹣3)的距离的最大值为2
的最大值,其几何意义是圆x2+y2=4上点(x,y)与定点(﹣1,﹣3)的距离的最大值为2![]() 2
2![]() ,
,
③当{|![]() |,|
|,|![]() |}={2,3},|
|}={2,3},|![]() |=1,则
|=1,则![]() ,
,
设![]() ,则x2+y2=1
,则x2+y2=1
∴![]() (2+x,3+y)
(2+x,3+y)
∴|![]() |
|![]() 的最大值,其几何意义是在圆x2+y2=1上取
的最大值,其几何意义是在圆x2+y2=1上取
点(x,y)与定点(﹣2,﹣3)的距离的最大值为1![]() 1
1![]()
∵![]() ,
,
故|![]() |的最大值为3
|的最大值为3![]() .
.
故答案为:3![]()


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC, ![]() .点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
(Ⅰ)求证:MN∥平面BDE;
(Ⅱ)求二面角C-EM-N的正弦值;
(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为![]() ,求线段AH的长.
,求线段AH的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表提供了工厂技术改造后某种型号设备的使用年限![]() 和所支出的维修费
和所支出的维修费![]() (万元)的几组对照数据:
(万元)的几组对照数据:
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
参考公式: ,
,![]() .
.
(1)若知道![]() 对
对![]() 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为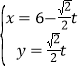 (t是参数),在以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为
(t是参数),在以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(Ⅰ)写出直线l的普通方程、曲线C的参数方程;
(Ⅱ)过曲线C上任意一点A作与直线l的夹角为45°的直线,设该直线与直线l交于点B,求![]() 的最值.
的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解人们对“延迟退休年龄政策”的态度,某部门从网年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:

(I)由频率分布直方图估计年龄的众数和平均数;
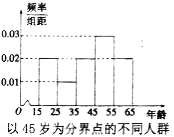
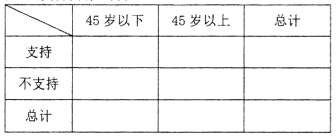
(II)由以上统计数据填2×2列联表,并判断是否有95%的把握认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
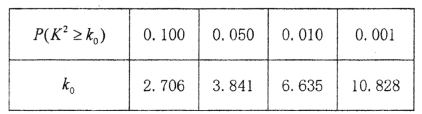
参考数据:
![]()
(III)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人.求抽到的2人中1人是45岁以下,另一人是45岁以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,
,![]() 为
为![]() 右支上的动点(非顶点),
右支上的动点(非顶点),![]() 为
为![]() 的内心.当
的内心.当![]() 变化时,
变化时,![]() 的轨迹为( )
的轨迹为( )
A.直线的一部分B.椭圆的一部分
C.双曲线的一部分D.无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市政府招商引资,为吸引外商,决定第一个月产品免税,某外资厂该第一个月A型产品出厂价为每件10元,月销售量为6万件;第二个月,当地政府开始对该商品征收税率为![]() ,即销售1元要征收
,即销售1元要征收![]() 元)的税收,于是该产品的出厂价就上升到每件
元)的税收,于是该产品的出厂价就上升到每件![]() 元,预计月销售量将减少p万件.
元,预计月销售量将减少p万件.
(1)将第二个月政府对该商品征收的税收y(万元)表示成p的函数,并指出这个函数的定义域;
(2)要使第二个月该厂的税收不少于1万元,则p的范围是多少?
(3)在第(2)问的前提下,要让厂家本月获得最大销售金额,则p应为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() :
:![]() ,
,![]() :
:![]() ,则下面结论正确的是( )
,则下面结论正确的是( )
A. 把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B. 把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com