
【题目】[选修4-4:坐标系与参数方程]在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+
(α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+ ![]() )=2
)=2 ![]() .
.
(1)写出C1的普通方程和C2的直角坐标方程;
(2)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标.
【答案】
(1)
解:曲线C1的参数方程为 ![]() (α为参数),
(α为参数),
移项后两边平方可得 ![]() +y2=cos2α+sin2α=1,
+y2=cos2α+sin2α=1,
即有椭圆C1: ![]() +y2=1;
+y2=1;
曲线C2的极坐标方程为ρsin(θ+ ![]() )=2
)=2 ![]() ,
,
即有ρ( ![]() sinθ+
sinθ+ ![]() cosθ)=2
cosθ)=2 ![]()
由x=ρcosθ,y=ρsinθ,可得x+y﹣4=0,
即有C2的直角坐标方程为直线x+y﹣4=0
(2)
解:由题意可得当直线x+y﹣4=0的平行线与椭圆相切时,
|PQ|取得最值.
设与直线x+y﹣4=0平行的直线方程为x+y+t=0,
联立 ![]() 可得4x2+6tx+3t2﹣3=0,
可得4x2+6tx+3t2﹣3=0,
由直线与椭圆相切,可得△=36t2﹣16(3t2﹣3)=0,
解得t=±2,
显然t=﹣2时,|PQ|取得最小值,
即有|PQ|= ![]() =
= ![]() ,
,
此时4x2﹣12x+9=0,解得x= ![]() ,
,
即为P( ![]() ,
, ![]() )
)
【解析】(1)运用两边平方和同角的平方关系,即可得到C1的普通方程,运用x=ρcosθ,y=ρsinθ,以及两角和的正弦公式,化简可得C2的直角坐标方程;
(2)由题意可得当直线x+y﹣4=0的平行线与椭圆相切时,|PQ|取得最值.设与直线x+y﹣4=0平行的直线方程为x+y+t=0,代入椭圆方程,运用判别式为0,求得t,再由平行线的距离公式,可得|PQ|的最小值,解方程可得P的直角坐标.
本题考查参数方程和普通方程的互化、极坐标和直角坐标的互化,同时考查直线与椭圆的位置关系,主要是相切,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,且
为正方形,且![]() ,其中
,其中![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,动点
的中点,动点![]() 在线段
在线段![]() 上运动时,下列四个结论:①
上运动时,下列四个结论:①![]() ;②
;②![]() ;③
;③![]() 面
面![]() ;④
;④![]() 面
面![]() ,
,
其中恒成立的为( )

A. ①③ B. ③④ C. ①④ D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米.开始时需将树苗集中放置在某一树坑旁边,使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小,这个最小值为 (米).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD,![]() 底面
底面![]() ,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.
,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.

(1)证明:MN//平面PAD;
(2)若PA与平面ABCD所成的角为![]() ,求四棱锥P-ABCD的体积V.
,求四棱锥P-ABCD的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1 , l2分别交C于A,B两点,交C的准线于P,Q两点.
(1)若F在线段AB上,R是PQ的中点,证明AR∥FQ;
(2)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2=4,点P为直线x+2y﹣9=0上一动点,过点P向圆C引两条切线PA、PB,A、B为切点,则直线AB经过定点( )
A.![]()
B.![]()
C.(2,0)
D.(9,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() +ax,aR,
+ax,aR,
(1)讨论函数f(x)的单调区间;
(2)求证:![]() ≥x;
≥x;
(3)求证:当a≥-2时,x[1,+ ∞),f(x)+lnx≥a+1恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求证:OE∥平面PDC;
(Ⅲ)求面PAD与面PBC所成角的大小.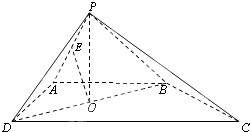
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com