练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆：上一点与两焦点构成的三角形的周长为,离心率为 .

    （1）求椭圆的方程；

    （2）设椭圆C的右顶点和上顶点分别为A、B，斜率为的直线l与椭圆C交于P、Q两点（点P在第一象限）.若四边形APBQ面积为，求直线l的方程.

    【答案】（1）；（2）。

    【解析】

    （ 1）设椭圆的半焦距为c，由已知得，又，a2=b2+c2，联立解出即可得出；

    （2）设直线方程为：代入椭圆并整理得：，利用韦达定理表示，分别计算Ａ，Ｂ到直线PQ的距离，即可表示四边形APBQ面积，从而得到直线l的方程.

    （1）由题设得，又，

    解得,

    ∴.

    故椭圆的方程为.

    （2）设直线方程为：代入椭圆并整理得：，

    设，则.

    ，

    到直线PQ的距离为，

    到直线PQ的距离为，

    又因为在第一象限, 所以，

    所以，

    所以，

    解得，

    所以直线方程为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】甲、乙两人练习罚球，每人练习6组，每组罚球20个，命中个数茎叶图如下：

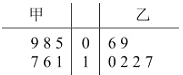
    （1）求甲命中个数的中位数和乙命中个数的众数；

    （2）通过计算，比较甲乙两人的罚球水平.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正四棱锥的底面正方形边长是3，是在底面上的射影，，是上的一点，过且与、都平行的截面为五边形．

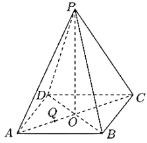
    （1）在图中作出截面，并写出作图过程；

    （2）求该截面面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，函数.

    （1）若，极大值；

    （2）若无零点，求实数的取值范围；

    （3）若有两个相异零点，，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数y=2cos（2x+）的图象向左平移个单位长度，得到函数y=f（x）的图象．

    （1）求f（x）的单调递增区间；

    （2）求f（x）在[0，]上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下表是某地某年月平均气温（华氏度）：

    月份

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    平均气温

    21.4

    26.0

    36.0

    48.8

    59.1

    68.6

    73.0

    71.9

    64.7

    53.5

    39.8

    27.7

    以月份为x轴（月份），以平均气温为y轴.

    （1）用正弦曲线去拟合这些数据；

    （2）估计这个正弦曲线的周期T和振幅A；

    （3）下面三个函数模型中，哪一个最适合这些数据？

    ①；②；③.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】每年春节，各地的餐馆都出现了用餐需预定的现象，致使一些人在没有预定的情况下难以找到用餐的餐馆，针对这种现象，专家对人们的用餐地点及性别作出调查，得到的情况如下表所示：

    在家用餐

    在餐馆用餐

    总计

    男性

    30

    女性

    40

    总计

    50

    100

    （1）完成上述列联表；

    （2）根据表中的数据，试通过计算判断是否有的把握说明用餐地点与性别有关？

    参考公式及数据：，其中.

    P(K2≥k0)

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k0

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，圆的参数方程为（为参数）.以坐标原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为.

    （1）求圆的普通方程和直线的直角坐标方程；

    （2）若直线与圆交于两点，是圆上不同于两点的动点，求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设a为实数，函数f（x）=ex﹣2x+2a，x∈R．

    （1）求f（x）的单调区间及极值；

    （2）求证：当a＞ln2﹣1且x＞0时，ex＞x2﹣2ax+1．

    查看答案和解析>>

    同步练习册答案