Question

【题目】在极坐标系中，圆C的极坐标方程为：ρ2=4ρ（cosθ+sinθ）﹣3．若以极点O为原点，极轴所在直线为x轴建立平面直角坐标系．
（Ⅰ）求圆C的参数方程；
（Ⅱ）在直角坐标系中，点P（x，y）是圆C上动点，试求x+2y的最大值，并求出此时点P的直角坐标．

Answer 1

【答案】解：（Ⅰ）∵圆C的极坐标方程为：ρ2=4ρ（cosθ+sinθ）﹣3．

∴直角坐标方程为：x2+y2﹣4x﹣4y+3=0，

即（x﹣2）2+（y﹣2）2=5为圆C的普通方程．

利用同角三角函数的平方关系可得：圆C的参数方程为 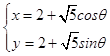（θ为参数）．

（Ⅱ）由（Ⅰ）可得，设点P（2+ cosθ，2+ sinθ），

∴x+2y=2+ cosθ+2（2+ ）=6+5

设sinα= ，则 ，

∴x+2y=6+5sin（θ+α），

当sin（θ+α）=1时，（x+2y）max=11，此时，θ+α= ，k∈Z．

∴sinθ=cosα= ，cosθ=sinα= ．

点P的直角坐标为（3，4）时，x+2y取得最大值11

【解析】（Ⅰ）由圆C的极坐标方程为：ρ2=4ρ（cosθ+sinθ）﹣3．利用互化公式可得直角坐标方程，再利用同角三角函数的平方关系可得圆C的参数方程．

（Ⅱ）由（Ⅰ）可得，设点P（2+ cosθ，2+ sinθ），可得x+2y=6+5 ，设sinα= ，则 ，可得x+2y=6+5sin（θ+α），再利用三角函数的单调性与值域即可得出最大值．