
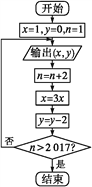
【题目】已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…,(xn,yn),…
(1)若程序运行中输出的一个数组是(9,t),求t的值.
(2)程序结束时,共输出(x,y)的组数为多少?
(3)写出程序框图的程序语句.
【答案】(1)-4;(2)1009;(3)答案见解析.
【解析】试题分析:
(1)利用所给的程序框图运行程序可得当x=9时,y=-4,则t的值为-4.
(2)结合程序的算法和循环结构的特点可知共输出(x,y)的组数为1009;
(3)将所给的程序框图翻译为算法语句,利用循环语句设计相应的程序即可,注意循环语句应设计为DO语句的形式.
试题解析:
(1)由程序框图知,当x=1时,y=0;
当x=3时,y=-2;
当x=9时,y=-4,所以t=-4.
(2)当n=1时,输出一对,当n=3时,又输出一对,…,当n=2 017时,输出最后一对,共输出(x,y)的组数为![]() 1 009.
1 009.
(3)程序框图的程序语句如下:
x=1
y=0
n=1
DO
PRINT (x,y)
n=n+2
x=3*x
y=y-2
LOOP UNTIL n>2 017
END


科目:高中数学 来源: 题型:
【题目】若函数y=f(x)在区间D上是增函数,且函数y=![]() 在区间D上是减函数,则称函数f(x)是区间D上的“H函数”.对于命题:
在区间D上是减函数,则称函数f(x)是区间D上的“H函数”.对于命题:
①函数f(x)=-x+![]() 是区间(0,1)上的“H函数”;
是区间(0,1)上的“H函数”;
②函数g(x)=![]() 是区间(0,1)上的“H函数”.下列判断正确的是( )
是区间(0,1)上的“H函数”.下列判断正确的是( )
A. ![]() 和
和![]() 均为真命题 B.
均为真命题 B. ![]() 为真命题,
为真命题,![]() 为假命题
为假命题
C. ![]() 为假命题,
为假命题,![]() 为真命题 D.
为真命题 D. ![]() 和
和![]() 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx,(a,b为常数,且a≠0)满足条件f(2-x)=f(x-1),且方程f(x)=x有两个相等的实根.
(1)求f(x)的解析式;
(2)设g(x)=kx+1,若F(x)=g(x)-f(x),求F(x)在[1,2]上的最小值;
(3)是否存在实数m,n(m<n),使f(x)的定义域和值域分别为[m,n]与[2m,2n],若存在,求出m,n的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中, ![]() ,
, ![]() ,以4个顶点为圆心的扇形的半径为1,若在该菱形中任意选取一点,该点落在阴影部分的概率为
,以4个顶点为圆心的扇形的半径为1,若在该菱形中任意选取一点,该点落在阴影部分的概率为![]() ,则圆周率
,则圆周率![]() 的近似值为( )
的近似值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】因为菱形的内角和为360°,
所以阴影部分的面积为半径为1的圆的面积,
故由几何概型可知 ,
,
解得![]() .选C。
.选C。
【题型】单选题
【结束】
12
【题目】已知函数f(x)= ,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)从区间![]() 内任意选取一个实数
内任意选取一个实数![]() ,求
,求![]() 的概率;
的概率;
(2)从区间![]() 内任意选取一个整数
内任意选取一个整数![]() ,求
,求![]() 的概率
的概率
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】试题(1)根据几何概型概率公式,分别求出满足不等式的![]() 的区间长度与区间总长度,求比值即可;(2) 区间
的区间长度与区间总长度,求比值即可;(2) 区间![]() 内共有
内共有![]() 个数,满足
个数,满足![]() 的整数为
的整数为![]() 共有
共有![]() 个,根据古典概型概率公式可得结果.
个,根据古典概型概率公式可得结果.
试题解析: (1)∵![]() ,∴
,∴![]() ,
,
故由几何概型可知,所求概率为 .
.
(2)∵![]() ,∴
,∴![]() ,
,
则在区间![]() 内满足
内满足![]() 的整数为5,6,7,8,9,共有5个,
的整数为5,6,7,8,9,共有5个,
故由古典概型可知,所求概率为![]() .
.
【方法点睛】本题題主要考查古典概型及“区间型”的几何概型,属于中档题. 解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,区间型,求与区间有关的几何概型问题关鍵是计算问题题的总区间 以及事件的区间;几何概型问题还有以下几点容易造成失分,在备考时要高度关注:(1)不能正确判断事件是古典概型还是几何概型导致错误;(2)基本裏件对应的区域测度把握不准导致错误 ;(3)利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误.
【题型】解答题
【结束】
18
【题目】已知函数f(x)=ax(a>0且a≠1)的图象过的(-2,16).
(1)求函数f(x)的解析式;
(2)若f(2m+5)<f(3m+3),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinxcosx+cos2x,x∈R.
sinxcosx+cos2x,x∈R.
(1)把函数f(x)的图象向右平移 ![]() 个单位,得到函数g(x)的图象,求g(x)在[0,
个单位,得到函数g(x)的图象,求g(x)在[0, ![]() ]上的最大值;
]上的最大值;
(2)在△ABC中,角A,B,C对应的三边分别为a,b,c,b= ![]() ,f(
,f( ![]() )=1,S△ABC=3
)=1,S△ABC=3 ![]() ,求a和c的值.
,求a和c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com