
分析 当x≥10时,f(x)=x-2=11;当1≤x<10时,f(x)=f(x+6),由1≤x<10,得7≤x+6<16,当7≤x+6<10时,f(x)=f(x+6)=f(x+12);当10≤x+6<16时,f(x)=f(x+6).由此能求出使f(x)=11成立的实数x的集合.
解答 解:∵f(x)=$\left\{\begin{array}{l}{x-2,(x≥10)}\\{f(x+6),(1≤x<10)}\end{array}\right.$,f(x)=11,
∴当x≥10时,f(x)=x-2=11,解得x=11;
当1≤x<10时,f(x)=f(x+6),
由1≤x<10,得7≤x+6<16,
当7≤x+6<10时,13≤x+12<16,
f(x)=f(x+6)=f(x+12)=x+12-2=11,解得x=1;
当10≤x+6<16时,f(x)=f(x+6)=x+6-2=11,解得x=7.
综上,使f(x)=11成立的实数x的集合为{1,7,13}.
故答案为:{1,7,13}.
点评 本题考查函数值的求法及应用,是基础题,解题时要认真审题,注意函数性质的合理运用.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,底面BCD是边长为2的等边三角形,侧棱AB=AD=$\sqrt{2}$,AC=2,O、E、F分别是BD、BC、AC的中点.
如图,在三棱锥A-BCD中,底面BCD是边长为2的等边三角形,侧棱AB=AD=$\sqrt{2}$,AC=2,O、E、F分别是BD、BC、AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
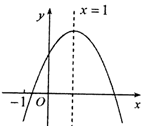 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;其中正确的结论为③④.(填序号)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;其中正确的结论为③④.(填序号)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
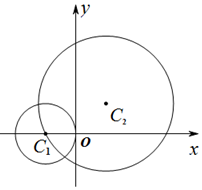 已知圆${C_1}:{x^2}+{y^2}+2x=0$,圆${C_2}:{x^2}+{y^2}-2x-2y-2=0$,C1,C2分别为两圆的圆心.
已知圆${C_1}:{x^2}+{y^2}+2x=0$,圆${C_2}:{x^2}+{y^2}-2x-2y-2=0$,C1,C2分别为两圆的圆心.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | (1,3) | B. | (-3,-1)∪(1,3) | C. | (-3,-1) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知△ABC和△EBC是边长为2的正三角形,平面EBC⊥平 面ABC,AD⊥平面ABC,且$AD=2\sqrt{3}$.
如图,已知△ABC和△EBC是边长为2的正三角形,平面EBC⊥平 面ABC,AD⊥平面ABC,且$AD=2\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lg101 | B. | 1 | C. | 2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $6\sqrt{2}$ | B. | $4\sqrt{5}$ | C. | $2\sqrt{34}$ | D. | 72 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com