
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且B=60°,c=4.
(Ⅰ)若b=6,求角C的正弦值及△ABC的面积;
(Ⅱ)若D,E在线段BC上,且BD=DE=EC, ![]() ,求AD的长.
,求AD的长.
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】假设某士兵远程射击一个易爆目标,射击一次击中目标的概率为![]() ,三次射中目标或连续两次射中目标,该目标爆炸,停止射击,否则就一直独立地射击至子弹用完.现有5发子弹,设耗用子弹数为随机变量X.
,三次射中目标或连续两次射中目标,该目标爆炸,停止射击,否则就一直独立地射击至子弹用完.现有5发子弹,设耗用子弹数为随机变量X.
(1)若该士兵射击两次,求至少射中一次目标的概率;
(2)求随机变量X的概率分布与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照[0,2],(2,4],…,(14,16]分成8组,制成了如图1所示的频率分布直方图. 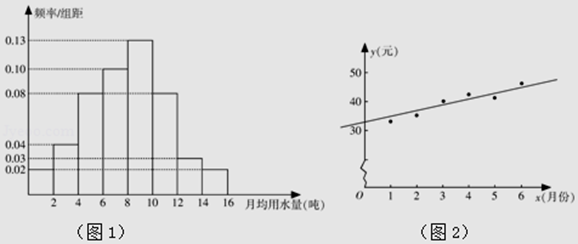
(Ⅰ)假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况.
( i)现从全市居民中依次随机抽取5户,求这5户居民恰好3户居民的月用水用量都超过12吨的概率;
(ⅱ)试估计全市居民用水价格的期望(精确到0.01);
(Ⅱ)如图2是该市居民李某2016年1~6月份的月用水费y(元)与月份x的散点图,其拟合的线性回归方程是 ![]() .若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD如图1中,AD= ![]() ,AB=2,E为AB中点,将△ADE沿DE折起到△PDE,所得四棱锥P﹣BCDE如图2所示.
,AB=2,E为AB中点,将△ADE沿DE折起到△PDE,所得四棱锥P﹣BCDE如图2所示.
(Ⅰ)若点M为PC中点,求证:BM∥平面PDE;
(Ⅱ)当平面PDE⊥平面BCDE时,求三棱锥E﹣PCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD﹣A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1= ![]() ,∠BAD=120°.
,∠BAD=120°.
(Ⅰ)求异面直线A1B与AC1所成角的余弦值;
(Ⅱ)求二面角B﹣A1D﹣A的正弦值.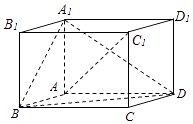
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com