(Ⅰ)解:因为数列{a
n}满足[2+(-1)
n+1]a
n+[2+(-1)
n]a
n+1=1+(-1)
n•3n,(*),且a
1=2,
所以将n=1代入(*)式,得3a
1+a
2=-2,故a
2=-8
将n=2代入(*)式,得a
2+3a
3=7,故a
3=5
(Ⅱ)证明:在(*)式中,用2n代换n,得[2+(-1)
2n+1]a
2n+[2+(-1)
2n]a
2n+1=1+(-1)
2n•6n,
即a
2n+3a
2n+1=1+6n ①,
再在(*)式中,用2n-1代换n,得[2+(-1)
2n]a
2n-1+[2+(-1)
2n-1]a
2n=1+(-1)
2n-1•(6n-3),
即3a
2n-1+a
2n=4-6n②,
①-②,得3(a
2n+1-a
2n-1)=12n-3,即b
n=4n-1
∴b
n+1-b
n=4,
∴{b
n}是等差数列;
(Ⅲ)解:因为a
1=2,由(Ⅱ)知,a
2k-1=a
1+(a
3-a
1)+…+(a
2k-1-a
2k-3)=(k-1)(2k-1)+2 ③,
将③代入②,得3(k-1)(2k-1)+6+a
2k=4-6k,即a
2k=-6k
2+3k-5
所以c
2k-1=a
2k-1+

(2k-1)
2=-4k
2-5k+

,c
2k=a
2k+

(2k)
2=-4k
2+3k-5,
则c
2k-1+c
2k=-2k-

,
所以S
2k=(c
1+c
2)+(c
3+c
4)+…+(c
2k-1+c
2k)=-k
2-
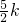
所以S
2k-1=S
2k-c
2k=(-k
2-
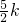
)-(-4k
2+3k-5)=3k
2-

+5
故S
n=
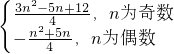
.
分析:(Ⅰ)将n=1,2分别代入[2+(-1)
n+1]a
n+[2+(-1)
n]a
n+1=1+(-1)
n•3n,即可求a
2,a
3的值;
(Ⅱ)在条件中,用2n代换n,用2n-1代换n,两式相减,可得b
n=4n-1,从而可得{b
n}是等差数列;
(Ⅲ)求得a
2k-1=a
1+(a
3-a
1)+…+(a
2k-1-a
2k-3)=(k-1)(2k-1)+2,a
2k=-6k
2+3k-5,从而可得c
2k-1=-4k
2-5k+

,c
2k=-4k
2+3k-5,则c
2k-1+c
2k=-2k-

,进而可得结论.
点评:本题考查数列递推式,考查等差数列的证明,考查数列的求和,正确运用数列递推式是关键,综合性强,难度较大.

 n2,求数列{cn}的前n项和Sn.
n2,求数列{cn}的前n项和Sn. (2k-1)2=-4k2-5k+
(2k-1)2=-4k2-5k+ ,c2k=a2k+
,c2k=a2k+ (2k)2=-4k2+3k-5,
(2k)2=-4k2+3k-5, ,
,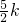
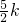 )-(-4k2+3k-5)=3k2-
)-(-4k2+3k-5)=3k2- +5
+5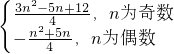 .
. ,c2k=-4k2+3k-5,则c2k-1+c2k=-2k-
,c2k=-4k2+3k-5,则c2k-1+c2k=-2k- ,进而可得结论.
,进而可得结论.
