
| 1 |
| 2 |
| 1 |
| 1-an |
| A、6 | B、-6 | C、2 | D、-2 |
| 1 |
| 2 |
| 1 |
| 1-an |
| 1 |
| 1-a1 |
| 1 | ||
1-
|
| 1 |
| 1-a2 |
| 1 |
| 1-2 |
| 1 |
| 1-a3 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x0x |
| a2 |
| y0y |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,2) | ||
| B、(2,+∞ | ||
C、(1,
| ||
D、(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| an |
| an+2 |
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
| bn |
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘成如图所示的茎叶图,若两种品牌销量的平均数为
某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘成如图所示的茎叶图,若两种品牌销量的平均数为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
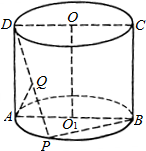 如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在
如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在 |
| AB |
 |
| AP |
| 1 |
| 3 |
 |
| APB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com