若函数f(x)=x3+a|x2-1|,a∈R,则对于不同的实数a,则函数f(x)的单调区间个数不可能是( )
A.1个
B.2个
C.3个
D.5个
【答案】
分析:先令a=0,即可排除A,再将函数化为分段函数,并分段求其导函数,得f′(x),最后利用分类讨论,通过画导函数f′(x)的图象判断函数f(x)的单调区间的个数,排除法得正确判断
解答:解:依题意:(1)当a=0时,f(x)=x
3,在(-∞,+∞)上为增函数,有一个单调区间 ①
当a≠0时,∵f(x)=x
3+a|x
2-1|a∈R
∴f(x)=
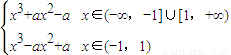
∴f′(x)=
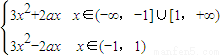
(2)当0<a<

时,∵-

<-
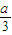
<0,0<
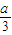
<

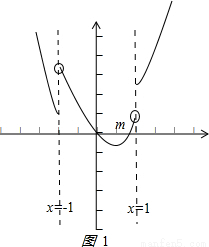
,∴导函数的图象如图1:(其中m为图象与x轴交点的横坐标)
∴x∈(-∞,0]时,f′(x)>0,x∈(0,m)时,f′(x)<0,x∈[m,+∞)时,f′(x)>0,
∴f(x)在x∈(-∞,0]时,单调递增,x∈(0,m)时,单调递减,x∈[m,+∞)时,单调递增,有3个单调区间 ②
(3)当a≥3时,∵-
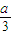
<-1,
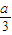
>1,∴导函数的图象如图2:
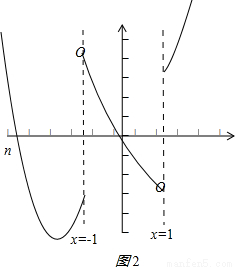
(其中n为x≤-1时图象与x轴交点的横坐标)
∴x∈(-∞,n]时,f′(x)>0,x∈(n,-1]时,f′(x)<0,x∈(-1,0)时,f′(x)>0,x∈[0,1)时,f′(x)<0,x∈[1,+∞)时,f′(x)>0
∴函数f(x)在x∈(-∞,n]时,单调递增,x∈(n,-1]时,单调递减,x∈(-1,0)时,单调递增,x∈[0,1)时,单调递减,x∈[1,+∞)时,单调递增,
有5个单调区间 ③
由①②③排除A、C、D,
故选B
点评:本题考查了含绝对值函数的单调区间的判断方法,利用导数研究三次函数单调区间的方法,函数与其导函数图象间的关系,排除法解选择题


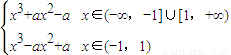
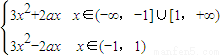
 时,∵-
时,∵- <-
<-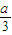 <0,0<
<0,0<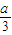 <
< ,∴导函数的图象如图1:(其中m为图象与x轴交点的横坐标)
,∴导函数的图象如图1:(其中m为图象与x轴交点的横坐标)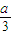 <-1,
<-1,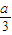 >1,∴导函数的图象如图2:
>1,∴导函数的图象如图2: (其中n为x≤-1时图象与x轴交点的横坐标)
(其中n为x≤-1时图象与x轴交点的横坐标)

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案