
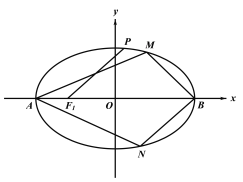
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,点
,点![]() 为椭圆的左、右顶点,点
为椭圆的左、右顶点,点![]() 是椭圆上一点,且直线
是椭圆上一点,且直线![]() 的倾斜角为
的倾斜角为![]() ,
,![]() ,已知椭圆的离心率为
,已知椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆上异于
为椭圆上异于![]() 的两点,若直线
的两点,若直线![]() 的斜率等于直线
的斜率等于直线![]() 斜率的
斜率的![]() 倍,求四边形
倍,求四边形![]() 面积的最大值.
面积的最大值.
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.
是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.

(Ⅰ)求证:PO平面![]() ;
;
(Ⅱ)求平面EFG与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,若存在,求线段
,若存在,求线段![]() 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由n(n∈N*)个正整数构成的集合A={a1,a2,…,an}(a1<a2<…<an,n≥3),记SA=a1+a2+…+an,对于任意不大于SA的正整数m,均存在集合A的一个子集,使得该子集的所有元素之和等于m.
(1)求a1,a2的值;
(2)求证:“a1,a2,…,an成等差数列”的充要条件是“![]() ”;
”;
(3)若SA=2020,求n的最小值,并指出n取最小值时an的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
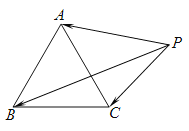
【题目】如图,![]() 是边长为1的正三角形,点P在
是边长为1的正三角形,点P在![]() 所在的平面内,且
所在的平面内,且![]() (a为常数),下列结论中正确的是( )
(a为常数),下列结论中正确的是( )
A.当![]() 时,满足条件的点P有且只有一个
时,满足条件的点P有且只有一个
B.当![]() 时,满足条件的点P有三个
时,满足条件的点P有三个
C.当![]() 时,满足条件的点P有无数个
时,满足条件的点P有无数个
D.当a为任意正实数时,满足条件的点总是有限个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,分别过
两点,分别过![]() ,
,![]() 作抛物线
作抛物线![]() 的切线,两切线交于点
的切线,两切线交于点![]() .
.
(1)若直线![]() 变动时,点
变动时,点![]() 始终在以
始终在以![]() 为直径的圆上,求动点
为直径的圆上,求动点![]() 的轨迹方程;
的轨迹方程;
(2)设圆![]() ,若直线
,若直线![]() 与圆
与圆![]() 相切于点
相切于点![]() (点
(点![]() 在线段
在线段![]() 上).是否存在点
上).是否存在点![]() 使得
使得![]() ?若存在,求出点
?若存在,求出点![]() 坐标,若不存在,说明理由.
坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的短轴长为
)的短轴长为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的标准方程;
(2)设M,N分别为椭圆C的左、右顶点,过点![]() 且不与x轴重合的直线
且不与x轴重合的直线![]() 与椭圆C相交于A,B两点是否存在实数t(
与椭圆C相交于A,B两点是否存在实数t(![]() ),使得直线
),使得直线![]() :
:![]() 与直线
与直线![]() 的交点P满足P,A,M三点共线?若存在,求出
的交点P满足P,A,M三点共线?若存在,求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子设备工厂生产一种电子元件,质量控制工程师要在产品出厂前将次品检出.估计这个厂生产的电子元件的次品率为0.2%,且电子元件是否为次品相互独立,一般的检测流程是:先把![]() 个
个![]() 电子元件串联起来成组进行检验,若检测通过,则全部为正品;若检测不通过,则至少有一个次品,再逐一检测,直到把所有的次品找出,若检验一个电子元件的花费为5分钱,检验一组(
电子元件串联起来成组进行检验,若检测通过,则全部为正品;若检测不通过,则至少有一个次品,再逐一检测,直到把所有的次品找出,若检验一个电子元件的花费为5分钱,检验一组(![]() 个)电子元件的花费为
个)电子元件的花费为![]() 分钱.
分钱.
(1)当![]() 时,估算一组待检元件中有次品的概率;
时,估算一组待检元件中有次品的概率;
(2)设每个电子元件检测费用的期望为![]() ,求
,求![]() 的表达式;
的表达式;
(3)试估计![]() 的值,使每个电子元件的检测费用的期望最小.(提示:用
的值,使每个电子元件的检测费用的期望最小.(提示:用![]() 进行估算)
进行估算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com