
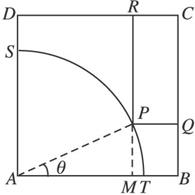
解:设∠PAB=θ,θ∈[0,![]() ]延长RP交AB于M,则AM=90cosθ,MP=90sinθ, ∴PQ=MB=100-90cosθ, PR=100-MP=100-90sinθ.
]延长RP交AB于M,则AM=90cosθ,MP=90sinθ, ∴PQ=MB=100-90cosθ, PR=100-MP=100-90sinθ.
∴S矩形=PQ·PR=10 000-9 000(sinθ+cosθ)+8 100sinθcosθ.
令t=sinθ+cosθ∈[1,![]() ],则sinθcosθ=
],则sinθcosθ=![]() ,
,
∴S矩形=10 000-9 000 t+8 100·![]()
=![]() (t-
(t-![]() )2+950.
)2+950.
∴当t=![]() 时,Smin=950 m2,
时,Smin=950 m2,
当t=![]() 时,Smax=(14 050-9 000
时,Smax=(14 050-9 000![]() )m2.
)m2.
思想方法小结:通过设角沟通AM与MP的联系,从而列出三角函数关系式,通过换元法转化为二次函数求解.在换元时,要注意三角函数的范围.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知ABCD是边长为1的正方形,AF⊥平面ABCD,CE∥AF,CE=λAF(λ>1).
如图,已知ABCD是边长为1的正方形,AF⊥平面ABCD,CE∥AF,CE=λAF(λ>1).3
| ||
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30°,PB与平面PCD所成的角为45°,求:
如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30°,PB与平面PCD所成的角为45°,求:查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.
如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com