求极限：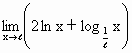
=________.
练习册系列答案
相关习题
科目：高中数学
来源：
题型：
已知数列{a
n}、{b
n}都是无穷等差数列，其中a
1=3，b
1=2，b
2是a
2与a
3的等差中项，且
=
，求极限
（
+
+…+
）的值．
查看答案和解析>>
科目：高中数学
来源：
题型：
已知数列{a
n}中，
a1=，a2=，且当n≥2，n∈N时，3a
n+1=4a
n-a
n-1．
（Ⅰ）求数列{a
n}的通项公式；
（Ⅱ）记
| n |
 |
| i=1 |
ai=a
1•a
2•a
3…a
n，n∈N，
（1）求极限
| n |
|
| i=1 |
ai；
（2）求证：2
| n |
|
| i=1 |
ai＞1．
查看答案和解析>>
科目：高中数学
来源：
题型：
设数列{a
n}，{b
n}满足a
1=1，b
1=0且
n=1，2，3，…（Ⅰ）求λ的值，使得数列{a
n+λb
n}为等比数列；
（Ⅱ）求数列{a
n}和{b
n}的通项公式；
（Ⅲ）令数列{a
n}和{b
n}的前n项和分别为S
n和S'
n，求极限
的值．
查看答案和解析>>
科目：高中数学
来源：
题型：
（2009•成都二模）已知数列{a
n}中，a
1=
，a
2=
且当n≥2，n∈N时，3a
n+1=4a-a
n-1
（I）求数列{a
n}的通项公式；
（Ⅱ）记
| n |
|
| i=1 |
ai=a
1•a
2•a
3…a
n，n∈N
* （1）求极限
| n |
|
| i=1 |
（2-2
i-1）
（2）对一切正整数n，若不等式λ
| n |
|
| i=1 |
a
i＞1（λ∈N
*）恒成立，求λ的最小值．
查看答案和解析>>
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
