
【题目】
设平面上向量![]() =(cosα,sinα) (0°≤α<360°),
=(cosα,sinα) (0°≤α<360°),![]() =(-
=(-![]() ,
,![]() ).
).
(1)试证:向量![]() 与
与![]() 垂直;
垂直;
(2)当两个向量![]() 与
与![]() 的模相等时,求角α.
的模相等时,求角α.
【答案】(1)见解析;(2)α=30°,或α=210°.
【解析】
本试题主要是考查了向量的数量积的运算,以及向量的数量积的性质的运用,以及三角函数的变形运用,和三角方程的求解的综合试题.
(1)根据已知要证明向量![]() 与
与![]() 垂直,则利用数量积为零即可.
垂直,则利用数量积为零即可.
(2)由|![]() |=1,|
|=1,|![]() |=1,且|
|=1,且|![]()
![]() +
+![]() |=|
|=|![]() -
-![]()
![]() |,利用模相等,则平方后相等来解得关于角α的方程,然后解三角方程得到角的值.
|,利用模相等,则平方后相等来解得关于角α的方程,然后解三角方程得到角的值.
解: (1)(![]() +
+![]() )·(
)·(![]() -
-![]() )=(cosα-
)=(cosα-![]() ,sinα+
,sinα+![]() )·(cosα+
)·(cosα+![]() ,sinα-
,sinα-![]() )
)
=(cosα-![]() )(cosα+
)(cosα+![]() )+(sinα+
)+(sinα+![]() )(sinα-
)(sinα-![]() )
)
=cos2α-![]() +sin2α-
+sin2α-![]() =0,
=0,
∴![]() ⊥
⊥![]() . ……4分
. ……4分
(2)由|![]() |=1,|
|=1,|![]() |=1,且|
|=1,且|![]()
![]() +
+![]() |=|
|=|![]() -
-![]()
![]() |,平方得(
|,平方得(![]()
![]() +
+![]() )2=(
)2=(![]() -
-![]() )2,
)2,
整理得2![]() 2-2
2-2![]() 2+4
2+4![]()
![]()
![]() =0①.
=0①.
∵|![]() |=1,|
|=1,|![]() |=1,∴①式化简得
|=1,∴①式化简得![]() ·
·![]() =0,
=0,
![]() ·
·![]() =(cosα,sinα)·(-
=(cosα,sinα)·(-![]() ,
,![]() )=-
)=-![]() cosα+
cosα+![]() sinα=0,即cos(60°+α)=0.
sinα=0,即cos(60°+α)=0.![]()
∵0°≤α<360°,∴可得α=30°,或α=210°


科目:高中数学 来源: 题型:
【题目】如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.
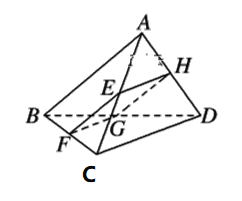
(1)求证:AB∥平面EFGH
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥S-ABC的底面是以AB为斜边的等腰直角三角形,SA=SB= SC=2,AB=2,设S、A、B、C四点均在以O为球心的某个球面上。则点O到平面ABC的距离为________________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,抛物线
,抛物线![]() 的焦点为
的焦点为![]() ,设
,设![]() 为抛物线
为抛物线![]() 上异于顶点的动点,直线
上异于顶点的动点,直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,连结
,连结![]() ,
,![]() ,并延长,分别交抛物线
,并延长,分别交抛物线![]() 与点
与点![]() ,
,![]() .
.
(1)当![]() 轴时,求直线
轴时,求直线![]() 与
与![]() 轴的交点的坐标;
轴的交点的坐标;
(2)设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试探索
,试探索![]() 是否为定值?若是,求出此定值;若不是,试说明理由.
是否为定值?若是,求出此定值;若不是,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,E,F分别为棱
的棱长为1,E,F分别为棱![]() ,AB上的点,下列说法正确的是________.(填上所有正确命题的序号)
,AB上的点,下列说法正确的是________.(填上所有正确命题的序号)
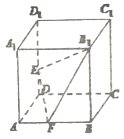
①![]() 平面
平面![]()
②在平面![]() 内总存在与平面
内总存在与平面![]() 平行的直线
平行的直线
③![]() 在侧面
在侧面![]() 上的正投影是面积为定值的三角形
上的正投影是面积为定值的三角形
④当E,F为中点时,平面![]() 截该正方体所得的截面图形是五边形
截该正方体所得的截面图形是五边形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,对任意
,对任意![]() ,有
,有![]() 成立.
成立.
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,求正整数
项和,求正整数![]() ,使得对任意
,使得对任意![]() ,
,![]() 恒成立;
恒成立;
(3)设![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,若对任意
项和,若对任意![]() 均有
均有![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 上的动点
上的动点![]() 到坐标原点
到坐标原点![]() 的距离
的距离![]() 的最大值;
的最大值;
(Ⅱ)若曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米,按交通法规限制50≤x≤100(单位:千米/时).假设汽油的价格是每升2元,而汽车每小时耗油![]() 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com