
 (其中e是自然对数的底数)
(其中e是自然对数的底数) ,求证:对于任意的t>-2,总存在x0∈(-2,t),满足
,求证:对于任意的t>-2,总存在x0∈(-2,t),满足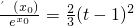 ,并确定这样的x0的个数.
,并确定这样的x0的个数.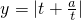 在t∈[1,e]时递增.
在t∈[1,e]时递增.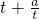 在t∈[1,e]时单调递增,得
在t∈[1,e]时单调递增,得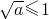 ,∴0<a≤1.
,∴0<a≤1.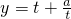 在t∈[1,e]时单调递增恒成立,故?t∈[1,e],
在t∈[1,e]时单调递增恒成立,故?t∈[1,e],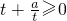 .
.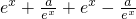 =2ex,∴φ(x)=(x2-3x+3)ex,∴
=2ex,∴φ(x)=(x2-3x+3)ex,∴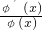 =x2-x.
=x2-x.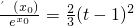 .
.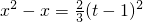 在区间(-2,t)内有实数解.
在区间(-2,t)内有实数解.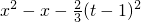 ,
,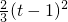 =-
=-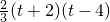 ,g(t)=
,g(t)=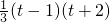 .
.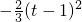 <0,
<0,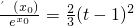 .
.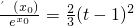 ,等价于证明:对任意的t>-2,方程
,等价于证明:对任意的t>-2,方程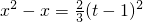 在区间(-2,t)内有实数解,通过对t分类讨论即可.
在区间(-2,t)内有实数解,通过对t分类讨论即可.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源: 题型:
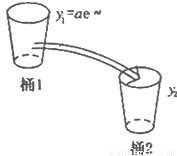
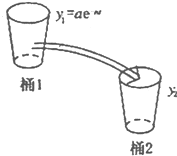 (2009•河北区二模)如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有a升水,桶2是空的,t分钟后桶1中剩余的水符合指数衰减曲线y1=ae-nt(其中n是常数,e是自对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求:
(2009•河北区二模)如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有a升水,桶2是空的,t分钟后桶1中剩余的水符合指数衰减曲线y1=ae-nt(其中n是常数,e是自对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求:| a | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
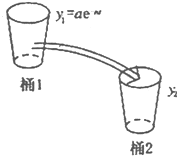 如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有a升水,桶2是空的,t分钟后桶1中剩余的水符合指数衰减曲线
如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有a升水,桶2是空的,t分钟后桶1中剩余的水符合指数衰减曲线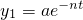 (其中n是常数,e是自对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求:
(其中n是常数,e是自对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求: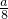 ?
?查看答案和解析>>
科目:高中数学 来源:2009年天津市河北区高考数学二模试卷(文科)(解析版) 题型:解答题
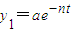 (其中n是常数,e是自对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求:
(其中n是常数,e是自对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求: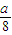 ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com