
【题目】已知函数f(x)=ax3﹣bx2+cx+b﹣a(a>0).
(1)设c=0. ①若a=b,曲线y=f(x)在x=x0处的切线过点(1,0),求x0的值;
②若a>b,求f(x)在区间[0,1]上的最大值.
(2)设f(x)在x=x1 , x=x2两处取得极值,求证:f(x1)=x1 , f(x2)=x2不同时成立.
【答案】
(1)解:当c=0时,f(x)=ax3﹣bx2+b﹣a.
①若a=b,则f(x)=ax3﹣ax2,
从而f'(x)=3ax2﹣2ax,
故曲线y=f(x)在x=x0处的切线方程为 ![]() =
= ![]() .
.
将点(1,0)代入上式并整理得 ![]() =x0(1﹣x0)(3x0﹣2),
=x0(1﹣x0)(3x0﹣2),
解得x0=0或x0=1.
②若a>b,则令f'(x)=3ax2﹣2bx=0,解得x=0或 ![]() .
.
(ⅰ)若b≤0,则当x∈[0,1]时,f'(x)≥0,
∴f(x)为区间[0,1]上的增函数,
∴f(x)的最大值为f(1)=0.
( ii)若b>0,列表:
x | 0 | (0, |
| ( | 1 |
f′(x) | 0 | ﹣ | 0 | + | |
f(x) | b﹣a<0 | 减函数 | 极小值 | 增函数 | 0 |
所以f(x)的最大值为f(1)=0.
综上,f(x)的最大值为0
(2)解:假设存在实数a,b,c,使得f(x1)=x1与f(x2)=x2同时成立.
不妨设x1<x2,则f(x1)<f(x2).
因为x=x1,x=x2为f(x)的两个极值点,
所以f'(x)=3ax2﹣2bx+c=3a(x﹣x1)(x﹣x2).
因为a>0,所以当x∈[x1,x2]时,f'(x)≤0,
故f(x)为区间[x1,x2]上的减函数,
从而f(x1)>f(x2),这与f(x1)<f(x2)矛盾,
故假设不成立.
既不存在实数a,b,c,使得f(x1)=x1,f(x2)=x2同时成立
【解析】(1)①计算f′(1),得出切线方程,代入点(1,0)列方程解出x0;②求出f(x)的极值点,判断两极值点的大小及与区间[0,1]的关系,从而得出f(x)在[0,1]上的单调性,得出最大值;(2)使用反证法证明.
【考点精析】本题主要考查了函数的极值与导数和函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;求函数
是极小值;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A.命题“若xy=0,则x=0”的否命题为:“若xy=0,则x≠0”
B.“若x+y=0,则x,y互为相反数”的逆命题为真命题
C.命题“x∈R,使得2x2﹣1<0”的否定是:“x∈R,均有2x2﹣1<0”
D.命题“若cosx=cosy,则x=y”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且(c﹣2a) ![]() =c
=c ![]()
![]()
(1)求B的大小;
(2)已知f(x)=cosx(asinx﹣2cosx)+1,若对任意的x∈R,都有f(x)≤f(B),求函数f(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(0,0),B(4,3),若A,B,C三点按顺时针方向排列构成等边三角形ABC,且直线BC与x轴交于点D.
(1)求cos∠CAD的值;
(2)求点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.
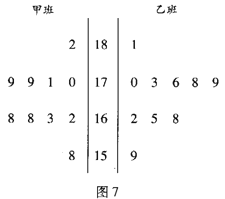
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正整数,其前n项和为Sn , an+1=  ,若S3=10,则S180=( )
,若S3=10,则S180=( )
A.600或900
B.900或560
C.900
D.600
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位,得到函数g(x)的图象,则下列关于g(x)叙述正确的是( )
个单位,得到函数g(x)的图象,则下列关于g(x)叙述正确的是( )
A.g(x)的最小正周期为2π
B.g(x)在 ![]() 内单调递增
内单调递增
C.g(x)的图象关于 ![]() 对称
对称
D.g(x)的图象关于 ![]() 对称
对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com