
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,关于
,关于![]() 的不等式
的不等式![]() 在区间
在区间![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,解关于
,解关于![]() 的不等式
的不等式![]() ;
;
(Ⅲ)若![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】
试题分析:(Ⅰ)![]() 在区间
在区间![]() 上恒成立,即
上恒成立,即![]() 在区间
在区间![]() 上恒成立.求
上恒成立.求![]() 在区间
在区间![]() 上的最小值即可.(Ⅱ)当
上的最小值即可.(Ⅱ)当![]() 时
时![]() 即
即![]() ,讨论当
,讨论当![]() 此不等式为一此不等式,当
此不等式为一此不等式,当![]() 时此不等式为一元二次不等式,方程的两根为
时此不等式为一元二次不等式,方程的两根为![]() 和1,需比较两根的大小再解不等式.(Ⅲ)属于线性规划问题,根据
和1,需比较两根的大小再解不等式.(Ⅲ)属于线性规划问题,根据![]() 和
和![]() 可得
可得![]() 的可行域,
的可行域,![]() ,
,![]() 表示动点
表示动点![]() 与定点
与定点![]() 距离的平方,根据线性规划先求得
距离的平方,根据线性规划先求得![]() 即可.
即可.
试题解析:(Ⅰ)不等式化为![]() ,即
,即![]() ,
,
即![]() 在区间
在区间![]() 上恒成立,2分
上恒成立,2分
由二次函数图象可知,当![]() 时,
时,![]() 有最小值
有最小值![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() .4分
.4分
(Ⅱ)当![]() 时,不等式
时,不等式![]() 化为
化为![]() ,5分
,5分
① 当![]() 时,不等式解集为
时,不等式解集为![]() ;6分
;6分
② 当![]() 时,不等式解集为
时,不等式解集为![]() ;7分
;7分
③ 当![]() 时,不等式
时,不等式![]() 化为
化为![]() ,
,
若![]() ,不等式解集为;
,不等式解集为;
若![]() ,不等式解集为
,不等式解集为![]() ;
;
若![]() ,不等式解集为
,不等式解集为![]() .
.
综上所述:
①当![]() 时,不等式解集为
时,不等式解集为![]() ;
;
②当![]() 时,不等式解集为
时,不等式解集为![]() ;
;
③当![]() 时,不等式解集为
时,不等式解集为![]() ;
;
④当![]() 时,不等式解集为;
时,不等式解集为;
⑤当![]() 时,不等式解集为
时,不等式解集为![]() .10分
.10分
(Ⅲ)由题有![]() 作出如图所示的平面区域:
作出如图所示的平面区域:
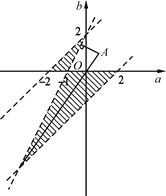
又![]() ,
,
因为![]() 表示动点
表示动点![]() 与定点
与定点![]() 距离的平方,
距离的平方,
所以,由图可知![]() 的范围为
的范围为![]() ,13分
,13分
所以,![]() 的取值范围为
的取值范围为![]() .14分
.14分


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某学校有2500名学生,其中高一1000人,高二900人,高三600人,为了了解学生的身体健康状况,采用分层抽样的方法,若从本校学生中抽取100人,从高一和高三抽取样本数分别为a,b,且直线ax+by+8=0与以A(1,﹣1)为圆心的圆交于B,C两点,且∠BAC=120°,则圆C的方程为( )
A.(x﹣1)2+(y+1)2=1
B.(x﹣1)2+(y+1)2=2
C.(x﹣1)2+(y+1)2= ![]()
D.(x﹣1)2+(y+1)2= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x+![]() )2+y2=16,点A(
)2+y2=16,点A(![]() ,0),Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E.
,0),Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E.
(1)求轨迹E的方程;
(2)过点P(1,0)的直线![]() 交轨迹E于两个不同的点A,B,△AOB(O是坐标原点)的面积S=
交轨迹E于两个不同的点A,B,△AOB(O是坐标原点)的面积S=![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只口袋有形状大小质地都相同的![]() 只小球,这
只小球,这![]() 只小球上分别标记着数字
只小球上分别标记着数字![]() .
.
甲乙丙三名学生约定:
(![]() )每个不放回地随机摸取一个球;
)每个不放回地随机摸取一个球;
(![]() )按照甲乙丙的次序一次摸取;
)按照甲乙丙的次序一次摸取;
(![]() )谁摸取的球的数字对打,谁就获胜.
)谁摸取的球的数字对打,谁就获胜.
用有序数组![]() 表示这个试验的基本事件,例如:
表示这个试验的基本事件,例如:![]() 表示在一次试验中,甲摸取的是数字
表示在一次试验中,甲摸取的是数字![]() ,乙摸取的是数字
,乙摸取的是数字![]() ,丙摸取的是数字
,丙摸取的是数字![]() ;
;![]() 表示在一次实验中,甲摸取的是数
表示在一次实验中,甲摸取的是数![]() ,乙摸取的是数字
,乙摸取的是数字![]() ,丙摸取的是数字
,丙摸取的是数字![]() .
.
(Ⅰ)列出基本事件,并指出基本事件的总数;
(Ⅱ)求甲获胜的概率;
(Ⅲ)写出乙获胜的概率,并指出甲乙丙三名同学获胜的概率与其摸取的次序是否有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)将函数y=sin2x的图象向左平移 ![]() 个单位,向下平移b个单位,得到函数y=f(x)的图象,求ab的值;
个单位,向下平移b个单位,得到函数y=f(x)的图象,求ab的值;
(Ⅲ)求函数f(x)在 ![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
①“若![]() , 则
, 则![]() 互为相反数”的逆命题;
互为相反数”的逆命题;
②“若两个三角形全等,则两个三角形的面积相等”的否命题;
③“若![]() ,则
,则![]() 有实根”的逆否命题;
有实根”的逆否命题;
④“若![]() 不是等边三角形,则
不是等边三角形,则![]() 的三个内角相等”逆命题;
的三个内角相等”逆命题;
其中真命题为( ).
A. ①② B. ②③ C. ①③ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于下列命题: ①在△ABC中,若sin2A=sin2B,则△ABC为等腰三角形;
②已知a,b,c是△ABC的三边长,若a=2,b=5, ![]() ,则△ABC有两组解;
,则△ABC有两组解;
③设 ![]() ,
, ![]() ,
, ![]() ,则a>b>c;
,则a>b>c;
④将函数 ![]() 图象向左平移
图象向左平移 ![]() 个单位,得到函数
个单位,得到函数 ![]() 图象.
图象.
其中正确命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com