
分析 (1)利用圆$G:{x^2}+{y^2}-x-\sqrt{3}y=0$经过点F,B.求出F,B,得到c,b,求出a.写出椭圆的方程.
(2)设直线l的方程为y=-(x-m)(m>2).联立方程组消去y,设C(x1,y1),D(x2,y2),利用韦达定理,结合数量积相遇0,求解m的范围.
解答 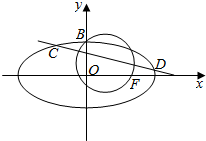 解:(1)∵圆$G:{x^2}+{y^2}-x-\sqrt{3}y=0$经过点F,B.
解:(1)∵圆$G:{x^2}+{y^2}-x-\sqrt{3}y=0$经过点F,B.
∴$F(1,0),B(0,\sqrt{3})$,
∴$c=1,b=\sqrt{3}$,∴a2=4.
故椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$,…(4分)
(2)设直线l的方程为y=-(x-m)(m>2).
由$\left\{{\begin{array}{l}{\frac{x^2}{4}+\frac{y^2}{3}=1}\\{y=-(x-m)}\end{array}}\right.$消去y得7x2-8mx+(4m2-12)=0,
设C(x1,y1),D(x2,y2),则${x_1}+{x_2}=\frac{8m}{7},{x_1}{x_2}=\frac{{4{m^2}-12}}{7}$,…(6分)
∴${y_1}{y_2}=[{-({x_1}-m)}]•[{-({x_2}-m)}]={x_1}{x_2}-m({x_1}+{x_2})+{m^2}$.
∵$\overrightarrow{FC}$=(x1-1,y1),$\overrightarrow{FD}$=(x2-1,y2),…(8分)
∴$\overrightarrow{FC}•\overrightarrow{FD}$=(x1-1)(x2-1)+y1y2)=x1x2-(x1+x2)+1+y1y2=$\frac{{7{m^2}-8m-17}}{7}$…(10分)
∵点F在圆G的内部,∴$\overrightarrow{FC}•\overrightarrow{FD}<0$,即$\frac{{7{m^2}-8m-17}}{7}<0$,
解得$\frac{{4-3\sqrt{15}}}{7}<m<\frac{{4+3\sqrt{15}}}{7}$,
由△=64m2-28(4m2-12)>0,解得$-\sqrt{7}<m<\sqrt{7}$.
又m>2,∴$2<m<\frac{{4+3\sqrt{15}}}{7}$,…(12分)
点评 本题考查椭圆的方程的求法,直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
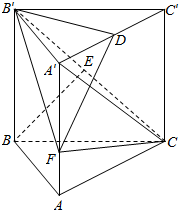 如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2,BB1=3,D为A1C1的中点,E为B1C的中点.
如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2,BB1=3,D为A1C1的中点,E为B1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 焦距 | B. | 准线 | C. | 顶点 | D. | 离心率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com