Question

已知向量

a

=(

3

sinωx，cosωx)，

b

=(cosωx，-cosωx)，(ω＞0)，函数f(x)=

a

•

b

+

1

2

的图象的两相邻对称轴间的距离为

π

4

，
（1）求ω；
（2）若x∈(0，

5

12

π)时，求函数f（x）的单调递增区间；
（3）若cosx≥

1

2

，x∈(0，π)，且f（x）=m有且仅有一个实根，求实数m的值．

Answer 1

分析：（1）由已知中向量

a

=(

3

sinωx，cosωx)，

b

=(cosωx，-cosωx)，(ω＞0)，函数f(x)=

a

•

b

+

1

2

，我们易求出函数的解析式，由函数f(x)=

a

•

b

+

1

2

的图象的两相邻对称轴间的距离为

π

4

，我们易得函数的最小正周期为

π

2

，由公式求出ω
（2）由正弦函数的单调性，令2kπ-

π

2

≤4x-

π

6

≤2kπ+

π

2

，k∈z，解出x的取值范围与所给的区间求交既得．
（3）由cosx≥

1

2

，x∈(0，π)，解出x的取值范围，作出符合条件的f（x）的图象，变f（x）=m有且仅有一个实根的问题为两个函数的图象有一个交点的问题，由图即可得到参数的取值范围．

解答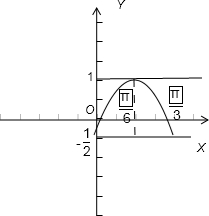：解：由题意，f(x)=

3

sinωx•cosωx-cos2ωx+

1

2

=

3

2

sin2ωx-

1+cos2ωx

2

+

1

2

=

3

2

sin2ωx-

1

2

cos2ωx

=sin(2ωx- π 6 )

．
（1）∵两相邻对称轴间的距离为

π

4

∴T=

2π

2ω

=

π

2

，∴ω=2
（2）由（1）知f(x)=sin(4x-

π

6

)，令2kπ-

π

2

≤4x-

π

6

≤2kπ+ 

π

2

，k∈z，解得

kπ

2

-

π

12

≤ x≤

kπ

2

+

π

6

，k∈z又x∈(0，

5

12

π)，故函数的单调递增区间是（0，

π

6

)
（3）∵cosx≥

1

2

，又因为余弦函数在（0，π）上是减函数，∴x∈(0，

π

3

]
令f(x)=

a

•

b

+

1

2

=sin(4x-

π

6

)，g（x）=m，在同一直角坐标系中
作出两个函数的图象，可知：m=1或m=-

1

2

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，求解的重点是从图象观察出函数的周期、最值、及点的坐标等几何特征来，然后根据相关的公式求出解析式中的参数，本题中考查了转化思想的运算，如第三小问中将方程有一个根的问题转化为两个函数的图象有一个交点的问题，从而可以用图象法解决问题，恰当的转化可以迅速达成问题的求解．本题运算量较大，求解时要严谨，避免马虎导致运算出错．