
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() (
(![]() )交于
)交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点,
为坐标原点,![]() .
.
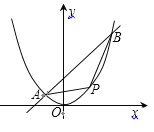
(1)求直线![]() 的方程和抛物线
的方程和抛物线![]() 的方程;
的方程;
(2)若抛物线![]() 上一动点
上一动点![]() 从
从![]() 到
到![]() 运动时(
运动时(![]() 不与
不与![]() 、
、![]() 重合),求
重合),求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() .
.
【解析】
1)设![]() ,
,![]() ,将直线方程代入抛物线的方程,运用韦达定理,由向量的坐标运算和点满足抛物线的方程,解方程可得
,将直线方程代入抛物线的方程,运用韦达定理,由向量的坐标运算和点满足抛物线的方程,解方程可得![]() ,
,![]() ,即可得到所求直线和抛物线的方程;
,即可得到所求直线和抛物线的方程;
(2)由直线和抛物线方程联立,运用韦达定理和弦长公式,可得![]() ,设
,设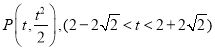 运用点到直线的距离公式,配方,由二次函数的最值求法,可得距离的最大值,进而得到
运用点到直线的距离公式,配方,由二次函数的最值求法,可得距离的最大值,进而得到![]() 面积的最大值.
面积的最大值.
(1)设![]() ,
,![]() ,
,
由![]() 得
得![]() ,由题意,
,由题意,![]() ,
,![]() ,
,
![]() ,即有
,即有![]() ,
,
则![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,
,
即![]() ,故
,故![]() ,
,![]() .
.
所以,直线![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() ;
;
(2)由![]() 得
得![]() ,
,![]() ,
,![]() ,
,
所以![]()
![]() ,
,
设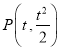 ,(
,(![]() ),
),
因为![]() 为定值,所以当点
为定值,所以当点![]() 到直线
到直线![]() 的距离
的距离![]() 最大时,
最大时,![]() 的面积取最大值.
的面积取最大值.
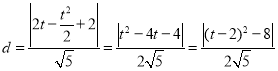 ,
,
因为![]() ,所以当
,所以当![]() 时,
时,![]() .
.
所以,当![]() 点坐标为
点坐标为![]() 时,
时,![]() 的面积取最大值,
的面积取最大值,
且![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】数列![]() 各项均不为0,前n项和为
各项均不为0,前n项和为![]() ,
,![]() ,
,![]() 的前n项和为
的前n项和为![]() ,且
,且![]()
(1)若数列![]() 共3项,求所有满足要求的数列;
共3项,求所有满足要求的数列;
(2)求证:![]() 是满足已知条件的一个数列;
是满足已知条件的一个数列;
(3)请构造出一个满足已知条件的无穷数列![]() ,并使得
,并使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李克强总理在很多重大场合都提出“大众创业,万众创新”.某创客,白手起家,2015年一月初向银行贷款十万元做创业资金,每月获得的利润是该月初投入资金的![]() .每月月底需要交纳房租和所得税共为该月全部金额(包括本金和利润)的
.每月月底需要交纳房租和所得税共为该月全部金额(包括本金和利润)的![]() ,每月的生活费等开支为3000元,余款全部投入创业再经营.如此每月循环继续.
,每月的生活费等开支为3000元,余款全部投入创业再经营.如此每月循环继续.
(1)问到2015年年底(按照12个月计算),该创客有余款多少元?(结果保留至整数元)
(2)如果银行贷款的年利率为![]() ,问该创客一年(12个月)能否还清银行贷款?
,问该创客一年(12个月)能否还清银行贷款?
查看答案和解析>>
科目:高中数学 来源: 题型:
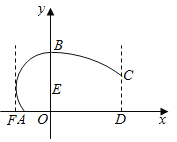
【题目】某地拟建造一座大型体育馆,其设计方案侧面的外轮廓如图所示,曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]() ;曲线
;曲线![]() 是抛物线
是抛物线![]() 的一部分;
的一部分;![]() ,且
,且![]() 恰好等于圆
恰好等于圆![]() 的半径.假定拟建体育馆的高
的半径.假定拟建体育馆的高![]() (单位:米,下同).
(单位:米,下同).
(1)若![]() ,
,![]() ,求
,求![]() 、
、![]() 的长度;
的长度;
(2)若要求体育馆侧面的最大宽度![]() 不超过
不超过![]() 米,求
米,求![]() 的取值范围;
的取值范围;
(3)若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 是圆
是圆![]() 上的一个动点,
上的一个动点,![]() 为圆心,线段
为圆心,线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 的交点为
的交点为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点(
两点(![]() 不经过
不经过![]() 点),且
点),且![]() ,证明:直线
,证明:直线![]() 经过定点,并写出该定点的坐标.
经过定点,并写出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的首项
的首项![]() 及数列的递推关系式
及数列的递推关系式![]() ;
;
(2)若数列![]() 成等比数列,求常数
成等比数列,求常数![]() 的值,并求数列
的值,并求数列![]() 的通项公式;
的通项公式;
(3)数列![]() 中是否存在三项
中是否存在三项![]() 、
、![]() 、
、![]() ,它们组成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
,它们组成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照如下规则构造数表:第一行是:2;第二行是:![]() ;即3,5,第三行是:
;即3,5,第三行是:![]() 即4,6,6,8;
即4,6,6,8;![]() (即从第二行起将上一行的数的每一项各项加1写出,再各项加3写出)
(即从第二行起将上一行的数的每一项各项加1写出,再各项加3写出)
2
3,5
4,6,6,8
5,7,7,9,7,9,9,11
……………………………………
若第![]() 行所有的项的和为
行所有的项的和为![]() .
.
(1)求![]() ;
;
(2)试求![]() 与
与![]() 的递推关系,并据此求出数列
的递推关系,并据此求出数列![]() 的通项公式;
的通项公式;
(3)设![]() ,求
,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】所谓声强,是指声音在传播途径上每1平方米面积上的声能流密度,用I表示,人类能听到的声强范围很广,其中能听见的1000Hz声音的声强(约10﹣12W/m2)为标准声强,记作I0,声强I与标准声强I0之比的常用对数称作声强的声强级,记作L,即L=lg![]() ,声强级L的单位名称为贝(尔),符号为B,取贝(尔)的十分之一作为响度的常用单位,称为分贝(尔).简称分贝(dB).《三国演义》中有张飞喝断当阳桥的故事,设张飞大喝一声的响度为140dB.一个士兵大喝一声的响度为90dB,如果一群士兵同时大喝一声相当一张飞大喝一声的响度,那么这群土兵的人数为( )
,声强级L的单位名称为贝(尔),符号为B,取贝(尔)的十分之一作为响度的常用单位,称为分贝(尔).简称分贝(dB).《三国演义》中有张飞喝断当阳桥的故事,设张飞大喝一声的响度为140dB.一个士兵大喝一声的响度为90dB,如果一群士兵同时大喝一声相当一张飞大喝一声的响度,那么这群土兵的人数为( )
A.1万B.2万C.5万D.10万
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 前20项的和
前20项的和![]() ;
;
(2)求通项公式![]() ;
;
(3)设![]() 的前
的前![]() 项和为
项和为![]() ,问:是否存在正整数
,问:是否存在正整数![]() 、
、![]() ,使得
,使得![]() ?若存在,请求出所有符合条件的正整数对
?若存在,请求出所有符合条件的正整数对![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com