Question

【题目】已知抛物线y2=2px（p＞0）上点M（3，m）到焦点F的距离为4．

（Ⅰ）求抛物线方程；

（Ⅱ）点P为准线上任意一点，AB为抛物线上过焦点的任意一条弦，设直线PA，PB，PF的斜率为k1，k2，k3，问是否存在实数λ，使得k1+k2=λk3恒成立．若存在，请求出λ的值；若不存在，请说明理由．

Answer 1

【答案】（1）抛物线方程为y2=4x；（2）见解析.

【解析】

由抛物线的定义，到焦点的距离等于到准线的距离即可求出，即可得到方程

求出焦点和准线，设出直线，联立方程，消去得到的方程，运用韦达定理，设，，，运用斜率公式，化简整理，注意点在抛物线上，且全部转化为的式子，即可判断

（I）抛物线y2=2px（p＞0）的焦点为（，0），准线为x=，

由抛物线的定义可知：4=3，p=2

∴抛物线方程为y2=4x；

（II）由于抛物线y2=4x的焦点F为（1，0），准线为x=﹣1，

设直线AB：x=my+1，与y2=4x联立，消去x，整理得：

y2﹣4my﹣4=0，

设A（x1，y1），B（x2，y2），P（﹣1，t），有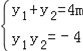

易知，而

==

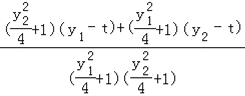
==2k3

∴存在实数λ=2，使得k1+k2=λk3恒成立．