解:A
t={y|y=f(x),点P(t,f(t)),Q(x,f(x))满足|PQ|≤

}表示以P点为圆心,

为半径的圆及其内部函数y=sin
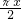
的图象上所有的点的纵坐标的集合,
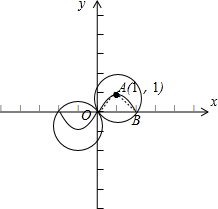
∵f(-2)=f(0)=f(2)=0,f(1)=1,f(-1)=-1,设O(0,0),A(1,1),B(2,0),则AO=AB=

,
∴M
t=

,
其中x
0是最高点Q的横坐标,
同理,m
t=
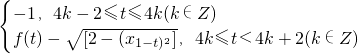
;
其中x
1是最低点Q的横坐标.
∴函数h(t)的最大值是2(t=4k或4k+2时取得),
单调增区间是(2k-1,2k).
分析:(1)理清A
t={y|y=f(x),点P(t,f(t)),Q(x,f(x))满足|PQ|≤

}的含义为:表示以P点为圆心,

为半径的圆及其内部函数y=sin
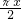
的图象上所有的点的纵坐标的集合,再利用正弦函数的周期性、单调性与最值可求得M
t,m
t,从而可求得函数h(t))=M
t-m
t的最大值;
(1)由(1)结合正弦函数的周期性与单调性即可求得函数h(t)的单调递增区间.
点评:本题考查函数的值域,着重考查抽象函数的理解与应用,明确A
t={y|y=f(x),点P(t,f(t)),Q(x,f(x))满足|PQ|≤√2}的含义是难点,也是解决问题的关键,考查抽象思维能力与综合运算能力,属于难题.

 x,任取t∈R,定义集合:At={y|y=f(x),点P(t,f(t)),Q(x,f(x))满足|PQ|≤
x,任取t∈R,定义集合:At={y|y=f(x),点P(t,f(t)),Q(x,f(x))满足|PQ|≤ }.设Mt,mt分别表示集合At中元素的最大值和最小值,记h(t)=Mt-mt.则
}.设Mt,mt分别表示集合At中元素的最大值和最小值,记h(t)=Mt-mt.则 }表示以P点为圆心,
}表示以P点为圆心, 为半径的圆及其内部函数y=sin
为半径的圆及其内部函数y=sin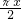 的图象上所有的点的纵坐标的集合,
的图象上所有的点的纵坐标的集合,
 ,
, ,
,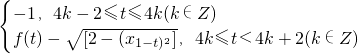 ;
; }的含义为:表示以P点为圆心,
}的含义为:表示以P点为圆心, 为半径的圆及其内部函数y=sin
为半径的圆及其内部函数y=sin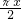 的图象上所有的点的纵坐标的集合,再利用正弦函数的周期性、单调性与最值可求得Mt,mt,从而可求得函数h(t))=Mt-mt的最大值;
的图象上所有的点的纵坐标的集合,再利用正弦函数的周期性、单调性与最值可求得Mt,mt,从而可求得函数h(t))=Mt-mt的最大值;

 教材全解字词句篇系列答案
教材全解字词句篇系列答案