
数列 1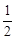 , 2
, 2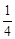 , 3
, 3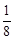 , 4
, 4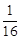 , 5
, 5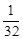 , …, 的前n项之和等于 .
, …, 的前n项之和等于 .
科目:高中数学 来源:2010-2011学年浙江省杭州市高三寒假作业数学卷一 题型:选择题
如果有穷数列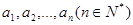 满足条件:
满足条件: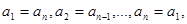
即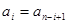 ,
,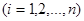 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列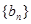 是项数不超过
是项数不超过 的“对称数列”,并使得
的“对称数列”,并使得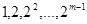 依次为该数列中连续的前
依次为该数列中连续的前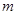 项,则数列
项,则数列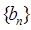 的前2009项和
的前2009项和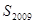 所有可能的取值的序号为
( )
所有可能的取值的序号为
( )
①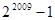 ②
②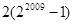 ③
③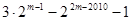 ④
④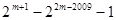
A.①②③ B. ②③④ C.①②④ D. ①③④
查看答案和解析>>
科目:高中数学 来源:2014届江西省上饶市等高一四校联考数学试卷 题型:解答题
将全体正整数组成的数列1,2,3,···,n,······进行如下的分组:(1),(2,3),(4,5,6),······.即第n组含有n个正整数(n=1,2,3, ·····),记第n组各数的和为 .
.
(Ⅰ)、求 的通项
的通项 ;
;
(Ⅱ)、求 的前n项和
的前n项和 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com