
| OF |
| OG |
| FG |
| OE |
| a2 |
| c |
| PF |
| c |
| a |
| PE |
| PE |
| OF |
| m |
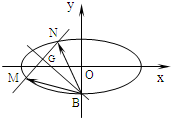
| BM |
| BN |
| BM |
| BN |
| OE |
| a2 |
| c |
| a2 |
| c |
| ||
| 2 |
| FG |
| (x-c)2+x2 |
2(x-
|
| ||
| 2 |
| ||
| 2 |
| 2 |
| OE |
| a2 |
| c |
| a2 |
| c |
| a2 |
| c |
| a |
| c |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 3 |
|
| 6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
| x1+x2 |
| 2 |
| 3km |
| 1+3k2 |
| 3k2m |
| 1+3k2 |
| m |
| 1+3k2 |
| m |
| 1+3k2 |
| 1 |
| k |
| 3km |
| 1+3k2 |
| BM |
| BN |
| m |
| 1+3k2 |
| 1 |
| k |
| 3km |
| 1+3k2 |
| 3m |
| 1+3k2 |
| 1+3k2 |
| 2 |
| 1+3k2 |
| 2 |
| BM |
| BN |
| BM |
| BN |
| ||
| 2 |
| |1+m| | ||
|
|1+
| ||
|
| 3 |
| 2 |
| 1+k2 |
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
(-
|
|
| 12(3k2-m2+1) |
| ||
| 1+3k2 |
12[3k2-(
|
| ||
|
| 1-k2 |
| 3 |
| 2 |
| 1+k2 |
3
| ||
| 2 |
| ||
|
| 1-k2 |
| 1 |
| 3 |
| ||
| 3 |
| 1+3k2 |
| 2 |
| 1+1 |
| 2 |
| ||
| 3 |



| Дкә¶ | ёЯЦРүОіМ | Дкә¶ | іхЦРүОіМ |
| ёЯТ» | ёЯТ»Гв·СүОіМНЖәцӘҰ | іхТ» | іхТ»Гв·СүОіМНЖәцӘҰ |
| ёЯ¶ю | ёЯ¶юГв·СүОіМНЖәцӘҰ | іх¶ю | іх¶юГв·СүОіМНЖәцӘҰ |
| ёЯИэ | ёЯИэГв·СүОіМНЖәцӘҰ | іхИэ | іхИэГв·СүОіМНЖәцӘҰ |
үЖДүӘғёЯЦРКэС§ АөФөӘғ МвРНӘғ
Ійүөөр°ёғНҢвОц>>
үЖДүӘғёЯЦРКэС§ АөФөӘғ МвРНӘғ
 ӘЁ2006•іҮСфЗшИэДӘӘ©ғҮКэy=fӘЁxӘ©µДНәПуИзНәЛщКңӘ¬Фтy=fӘЁxӘ©µДµәғҮКэy=fҰдӘЁxӘ©µДНәПуүЙТФКЗӘЁҰҰҰҰӘ©
ӘЁ2006•іҮСфЗшИэДӘӘ©ғҮКэy=fӘЁxӘ©µДНәПуИзНәЛщКңӘ¬Фтy=fӘЁxӘ©µДµәғҮКэy=fҰдӘЁxӘ©µДНәПуүЙТФКЗӘЁҰҰҰҰӘ©Ійүөөр°ёғНҢвОц>>
үЖДүӘғёЯЦРКэС§ АөФөӘғ МвРНӘғ
| 1 | 4 |
Ійүөөр°ёғНҢвОц>>
үЖДүӘғёЯЦРКэС§ АөФөӘғ МвРНӘғ
Ійүөөр°ёғНҢвОц>>
үЖДүӘғёЯЦРКэС§ АөФөӘғ МвРНӘғ
 ӘЁ2006•іҮСфЗшИэДӘӘ©ТСЦҒӘғФЪХэИэАвЦщABC-A1B1C1ЦРӘ¬AB=aӘ¬AA1=2aӘ¬DҰұE·Ц±рКЗІаАвBB1ғНAC1µДЦРµгӘ®
ӘЁ2006•іҮСфЗшИэДӘӘ©ТСЦҒӘғФЪХэИэАвЦщABC-A1B1C1ЦРӘ¬AB=aӘ¬AA1=2aӘ¬DҰұE·Ц±рКЗІаАвBB1ғНAC1µДЦРµгӘ®Ійүөөр°ёғНҢвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
ғю±±КҰ»ӨБҒНшОӨ·ЁғНІ»БәРЕПұңЩ±ЁЖҢМЁ | НшЙПУРғ¦РЕПұңЩ±ЁЧЁЗш | µзРЕХ©ЖңЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРғ¦РЕПұңЩ±ЁЧЁЗш | ЙжЖуЗЦИЁңЩ±ЁЧЁЗш
ОӨ·ЁғНІ»БәРЕПұңЩ±Ёµз»°Әғ027-86699610 ңЩ±ЁУКПдӘғ58377363@163.com