练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．在△ABC中，∠BAC=120°，AB=2，AC=1，D是边BC上的点，且|BD|=2|DC|，则$\overrightarrow{AD}$•$\overrightarrow{BC}$的值为（　　）
    A．0B．1C．$\frac{1}{3}$D．-$\frac{1}{3}$

    分析 建立平面直角坐标系，求出向量坐标，代入公式计算．

    解答 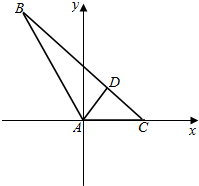解：建立如图所示的坐标系，则A（0，0），B（-1，$\sqrt{3}$），C（1，0），D（$\frac{1}{3}$，$\frac{\sqrt{3}}{3}$）．
    ∴$\overrightarrow{AD}$=（$\frac{1}{3}$，$\frac{\sqrt{3}}{3}$），$\overrightarrow{BC}$=（2，-$\sqrt{3}$）．∴$\overrightarrow{AD}$•$\overrightarrow{BC}$=$\frac{1}{3}×2$-$\frac{\sqrt{3}}{3}$×$\sqrt{3}$=-$\frac{1}{3}$．
    故选：D．

    点评 本题考查了平面向量的数量积运算，建立坐标系可使计算简便．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    11．已知，A为△ABC的一个内角，cosA+sinA=$\frac{1}{5}$．求：
    （1）tanA的值；
    （2）$\frac{sinA+2cosA}{sinA-cosA}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知{an}是公差为d的等差数列，它的前n项和为Sn，S4=2S2+4，${b_n}=\frac{{1+{a_n}}}{a_n}$．
    （1）求公差d的值；
    （2）若${a_1}=-\frac{5}{2}$，求数列{bn}中的最大项和最小项的值；
    （3）若对任意的n∈N*，都有bn≤b8成立，求a1的取值范围．
    （4）若对任意的n∈N*，数列{bn}中最小值为b8，求a1的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．圆心在（1，1）的圆截直线y=x-2所得的弦长为2$\sqrt{2}$，则这个圆的方程为（x-1）2+（y-1）2=4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．将函数f（x）=$\sqrt{3}$sin3x+cos3x的图象向左平移$\frac{π}{6}$个单位得到函数g（x）的图象，关于函数g（x），下列说法正确的是（　　）
    A．在[$\frac{π}{4}$，$\frac{π}{2}$]上是增函数
    B．其图象关于直线x=-$\frac{π}{4}$对称
    C．函数g（x）是奇函数
    D．当x$∈[\frac{π}{3}，\frac{4π}{9}]$时，函数g（x）的值域是[-$\sqrt{3}$，0]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．用与球心距离为2的平面去截球，所得的截面面积为π，则球的表面积为（　　）
    A．$\frac{20π}{3}$B．20πC．12πD．100π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．株洲市某中学利用周末组织教职员工进行了一次秋季登石峰山健身的活动，有N人参加，现将所有参加人员按年龄情况分为[20，25），[25，30），[30，35]，[35，40），[40，45），[45，50），[50，55）等七组，其频率分布直方图如图所示．已知[35，40）之间的参加者有8人．
    （1）求N和[30，35]之间的参加者人数N1；
    （2）已知[30，35）和[35，40）之间各有2名数学教师，现从这两个组中各选取2人担任接待工作，设两组的选择互不影响，求两组选出的人中都至少有1名数学教师的概率？
    （3）组织者从[45，50）之间的参加者（其中共有4名女教师，其余全为男教师）中随机选取3名担任后勤保障工作，其中女教师的人数为ξ，求ξ的分布列和均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知在正四面体A-BCD中，E，F分别是线段AB，CD的中点，则直线CE，AF的夹角的余弦值是（　　）
    A．$\frac{{\sqrt{6}}}{3}$B．$\frac{{\sqrt{3}}}{3}$C．$\frac{1}{3}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知a＜b＜0，$\root{3}{a}$-$\root{3}{b}$=m，$\root{3}{a-b}$=n，则有（　　）
    A．m＞nB．m＜nC．m=nD．m≤n

    查看答案和解析>>

    同步练习册答案