
【题目】设定义在![]() 上的函数
上的函数![]() 满足任意
满足任意![]() 都有
都有![]() ,且
,且![]() 时,
时,![]() ,则
,则![]() ,
,![]() ,
,![]() 的大小关系是( )
的大小关系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
函数f(x)满足f(t+2)=![]() ,可得f(x)是周期为4的函数.6f(2017)=6f(1),3f(2018)
,可得f(x)是周期为4的函数.6f(2017)=6f(1),3f(2018)
=3f(2),2f(2019)=2f(3).令g(x)=![]() ,x∈(0,4],则g′(x)=
,x∈(0,4],则g′(x)=![]() >0,利
>0,利
用其单调性即可得出.
函数f(x)满足f(t+2)=![]() ,可得f(t+4)=
,可得f(t+4)=![]() =f(t),∴f(x)是周期为4的函数.
=f(t),∴f(x)是周期为4的函数.
6f(2017)=6f(1),3f(2018)=3f(2),2f(2019)=2f(3).
令g(x)=![]() ,x∈(0,4],则g′(x)=
,x∈(0,4],则g′(x)=![]() ,
,
∵x∈(0,4]时,![]() ,
,
∴g′(x)>0,g(x)在(0,4]递增,
∴f(1)<![]() <
<![]() ,
,
可得:6f(1)<3f(2)<2f(3),即6f(2017)<3f(2018)<2f(2019).
故答案为:A


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,点
,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为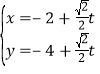 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知曲线
轴正半轴为极轴,建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,记直线
,记直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)求曲线![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)证明:![]() 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全国第五个“扶贫日”到来之前,某省开展“精准扶贫,携手同行”的主题活动,某贫困县调查基层干部走访贫困户数量.![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从
镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从![]() 三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,
三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
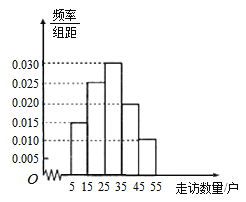
(1)求这40人中有多少人来自![]() 镇,并估计
镇,并估计![]() 三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
(2)如果把走访贫困户达到或超过25户视为工作出色,以频率估计概率,从![]() 三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为
三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() 且在
且在![]() 轴上截得的弦长为4。
轴上截得的弦长为4。
(1)求动圆![]() 的圆心
的圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的动直线与曲线
的动直线与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 在曲线
在曲线![]() 上,使得
上,使得![]() 的重心
的重心![]() 在
在![]() 轴上,直线
轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,且点
,且点![]() 在点
在点![]() 的右侧,记
的右侧,记![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市自2014年至2019年每年年初统计得到的人口数量如表所示.
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数(单位:万) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)设第![]() 年的人口数量为
年的人口数量为![]() (2014年为第1年),根据表中的数据,描述该城市人口数量和2014年至2018年每年该城市人口的增长数量的变化趋势;
(2014年为第1年),根据表中的数据,描述该城市人口数量和2014年至2018年每年该城市人口的增长数量的变化趋势;
(2)研究统计人员用函数![]() 拟合该城市的人口数量,其中
拟合该城市的人口数量,其中![]() 的单位是年.假设2014年初对应
的单位是年.假设2014年初对应![]() ,
,![]() 的单位是万.设
的单位是万.设![]() 的反函数为
的反函数为![]() ,求
,求![]() 的值(精确到0.1),并解释其实际意义.
的值(精确到0.1),并解释其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生鲜批发店每天从蔬菜生产基地以5元/千克购进某种绿色蔬菜,售价8元/千克,若每天下午4点以前所购进的绿色蔬菜没有售完,则对未售出的绿色蔬菜降价处理,以3元/千克出售.根据经验,降价后能够把剩余蔬菜全部处理完毕,且当天不再进货.该生鲜批发店整理了过往30天(每天下午4点以前)这种绿色蔬菜的日销售量(单位:千克)得到如下统计数据(视频率为概率)(注:x,y∈N*)
每天下午4点前销售量 | 350 | 400 | 450 | 500 | 550 |
天数 | 3 | 9 | x | y | 2 |
(1)求在未来3天中,至少有1天下午4点前的销售量不少于450千克的概率.
(2)若该生鲜批发店以当天利润期望值为决策依据,当购进450千克比购进500千克的利润期望值大时,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com