
 如图,在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,CC1=2AC=2.
如图,在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,CC1=2AC=2.分析 (Ⅰ)取BC中点E连结AE,三棱锥C1-CB1A的体积${V_{{C_1}-AC{B_1}}}={V_{A-C{B_1}{C_1}}}=\frac{1}{3}{S_{△C{B_1}{C_1}}}•|{AE}|$,由此能求出结果.
(Ⅱ)在矩形BB1C1C中,连结EC1,推导出Rt△C1CE∽Rt△CBF,从而CF⊥EC1,再求出AE⊥CF,由此得到在BB1上取F,使得$BF=\frac{1}{4}$,连结CF,CF即为所求直线.
解答 解:(Ⅰ)取BC中点E连结AE,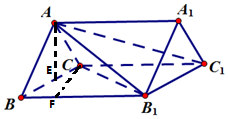
在等边三角形ABC中,AE⊥BC,
又∵在直三棱柱ABC-A1B1C1中,
侧面BB1CC1⊥面ABC,
面BB1CC1∩面ABC=BC,∴AE⊥面BB1CC1,
∴AE为三棱锥B1-ACC1的高,
又∵AB=AC=BC=1,∴$AE=\frac{{\sqrt{3}}}{2}$,
又∵底面CC1B1为直角三角形,
∴${S}_{△C{C}_{1}B}$=$\frac{1}{2}×{C}_{1}C×{B}_{1}{C}_{1}$=$\frac{1}{2}×2×1$=1,
∴三棱锥C1-CB1A的体积${V_{{C_1}-AC{B_1}}}={V_{A-C{B_1}{C_1}}}=\frac{1}{3}{S_{△C{B_1}{C_1}}}•|{AE}|$=$\frac{1}{3}×1×\frac{{\sqrt{3}}}{2}=\frac{{\sqrt{3}}}{6}$.
(Ⅱ)作法:在BB1上取F,使得$BF=\frac{1}{4}$,连结CF,CF即为所求直线.
证明:如图,在矩形BB1C1C中,连结EC1,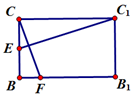 ∵$\frac{{C{C_1}}}{CE}=\frac{2}{{\frac{1}{2}}}=4$,$\frac{CB}{BF}=\frac{1}{{\frac{1}{4}}}=4$,∴$\frac{{C{C_1}}}{CE}=\frac{CB}{BF}$,
∵$\frac{{C{C_1}}}{CE}=\frac{2}{{\frac{1}{2}}}=4$,$\frac{CB}{BF}=\frac{1}{{\frac{1}{4}}}=4$,∴$\frac{{C{C_1}}}{CE}=\frac{CB}{BF}$,
∴Rt△C1CE∽Rt△CBF,∴∠CC1E=∠BCF,
又∵∠BCF+∠FCC1=90°,∴∠CC1E+∠FCC1=90°,∴CF⊥EC1,
又∵AE⊥面BB1C1C,而CF?面BB1C1C,∴AE⊥CF,
又∵AE∩EC1=E,∴CF⊥面AEC1,
又∵AC1?面AEC1,∴CF⊥AC1.
点评 本题考查三棱锥的求法,考查满足线线垂直的点的确定与求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
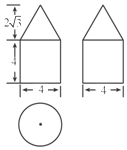 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的体积为( )
如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的体积为( )| A. | 16π+$\sqrt{3}π$ | B. | 16π+8$\sqrt{3}$π | C. | 16π+$\frac{8}{3}\sqrt{3}π$ | D. | 16π+$\frac{4}{3}\sqrt{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,E,E,G,H分别是棱AB,BB1,BC,CC1的中点,∠ABC=90°.则异面直线EF和GH所成的角是( )
如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,E,E,G,H分别是棱AB,BB1,BC,CC1的中点,∠ABC=90°.则异面直线EF和GH所成的角是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,上顶点为B,直线l:y=$\frac{1}{2}$x与椭圆E交于C,D两点,且△BCD的面积为$\sqrt{2}$.
在平面直角坐标系xOy中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,上顶点为B,直线l:y=$\frac{1}{2}$x与椭圆E交于C,D两点,且△BCD的面积为$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S2017=2017,a1007>a1011 | B. | S2017=-2017,a1007>a1011 | ||
| C. | S2017=2017,a1007<a1011 | D. | S2017=-2017,a1007<a1011 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com