练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数，，若对任意，都有成立，则实数的取值范围是（ ）

    A.B.C.D.

    【答案】D

    【解析】

    试题求函数f（x）定义域，及f（﹣x）便得到f（x）为奇函数，并能够通过求f′（x）判断f（x）在R上单调递增，从而得到sinθ＞m﹣1，也就是对任意的都有sinθ＞m﹣1成立，根据0＜sinθ≤1，即可得出m的取值范围．

    f（x）的定义域为R，f（﹣x）=﹣f（x）；

    f′（x）=ex+e﹣x＞0；

    ∴f（x）在R上单调递增；

    由f（sinθ）+f（1﹣m）＞0得，f（sinθ）＞f（m﹣1）；

    ∴sinθ＞m﹣1；

    即对任意θ∈都有m﹣1＜sinθ成立；

    ∵0＜sinθ≤1；

    ∴m﹣1≤0；

    ∴实数m的取值范围是（﹣∞，1]．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C所对的边分别为a，b，c，已知bcos（A）asin（B）＝0，且sinA，sinB，2sinC成等比数列．

    （1）求角B；

    （2）若a+c＝λb（λ∈R），求λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】研学旅行是研究性学习和旅行体验相结合的校外教育活动，继承和发展了我国传统游学、“读万卷书，行万里路”的教育理念和人文精神，成为素质教育的新内容和新方式，提升中小学生的自理能力、创新精神和实战能力，是综合实战育人的有效途径，为了了解某校高二年级600名学生在一次研学旅行活动中的武术表演情况，研究人员在该校高二学生中随机抽取了10名学生的武术表演成绩进行统计，统计结果如图所示（满分100分），已知这10名学生或武术表演的平均成绩为85分.

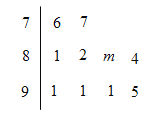
    （1）求m的值；

    （2）为了研究高二男、女生的武术表演情况，现对该校高二所有学生的武术表演成绩进行分类统计，得到的数据如下表所示：

    男生

    女生

    合计

    武术表演成绩超过80分

    150

    武术表演成绩不超过80分

    100

    合计

    已知随机抽取这600名学生中的一名学生，抽到武术表演成绩超过80分的学生概率是，根据已知条件完成上面列联表，并据此判断是否有的把握认为武术表演成绩超过80分与性别具有相关性.

    参考公式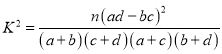：，其中.

    临界值表：

    P（）

    0.100

    0.050

    0.010

    0.001

    2.706

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某亲子游戏结束时有一项抽奖活动，抽奖规则是：盒子里面共有4个小球，小球上分别写有0，1，2，3的数字，小球除数字外其他完全相同，每对亲子中，家长先从盒子中取出一个小球，记下数字后将小球放回，孩子再从盒子中取出一个小球，记下小球上数字将小球放回．抽奖活动的奖励规则是：①若取出的两个小球上数字之积大于4，则奖励飞机玩具一个；②若取出的两个小球上数字之积在区间上，则奖励汽车玩具一个；③若取出的两个小球上数字之积小于1，则奖励饮料一瓶．

    （1）求每对亲子获得飞机玩具的概率；

    （2）试比较每对亲子获得汽车玩具与获得饮料的概率，哪个更大？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数在定义域上的导函数为，若函数没有零点，且，当在上与在上的单调性相同时，则实数的取值范围是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若的定义域，值域都是，求的值；

    （2）当时，讨论在区间上的值域.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝a1nx﹣ax+1（a∈R且a≠0）．

    （1）求函数f（x）的单调区间；

    （2）求证：（n≥2，n∈N*）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱锥P﹣ABC中，AB＝1，BC＝2，AC，PC，PA，PB，E是线段BC的中点．

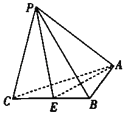
    （1）求点C到平面APE的距离d；

    （2）求二面角P﹣EA﹣B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场周年庆，准备提供一笔资金，对消费满一定金额的顾客以参与活动的方式进行奖励.顾客从一个装有大小相同的2个红球和4个黄球的袋中按指定规则取出2个球，根据取到的红球数确定奖励金额，具体金额设置如下表：

    取到的红球数

    0

    1

    2

    奖励（单位：元）

    5

    10

    50

    现有两种取球规则的方案：

    方案一：一次性随机取出2个球；

    方案二：依次有放回取出2个球.

    （Ⅰ）比较两种方案下，一次抽奖获得50元奖金概率的大小；

    （Ⅱ）为使得尽可能多的人参与活动，作为公司的负责，你会选择哪种方案？请说明理由.

    查看答案和解析>>

    同步练习册答案