Question

【题目】2019年春节期间，我国高速公路继续执行“节假日高速免费政策”.某路桥公司为掌握春节期间车辆出行的高峰情况，在某高速收费点处记录了大年初三上午9:20～10:40这一时间段内通过的车辆数，统计发现这一时间段内共有600辆车通过该收费点，它们通过该收费点的时刻的频率分布直方图如图所示，其中时间段9:20～9：40记作区间，9:40～10:00记作，10:00～10:20记作，10:20～10:40记作.比方：10点04分，记作时刻64.

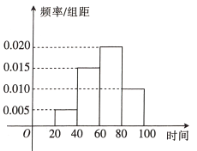
（1）估计这600辆车在9:20～10:40时间段内通过该收费点的时刻的平均值（同一组中的数据用该组区间的中点值代表）；

（2）为了对数据进行分析，现采用分层抽样的方法从这600辆车中抽取10辆，再从这10辆车中随机抽取4辆，记为9:20～10:00之间通过的车辆数，求的分布列与数学期望；

（3）由大数据分析可知，车辆在春节期间每天通过该收费点的时刻服从正态分布，其中可用这600辆车在9:20～10:40之间通过该收费点的时刻的平均值近似代替，可用样本的方差近似代替（同一组中的数据用该组区间的中点值代表），已知大年初五全天共有1000辆车通过该收费点，估计在9:46～10:40之间通过的车辆数（结果保留到整数）.

参考数据：若，则，，.

Answer 1

【答案】（1）10点04分；（2）详见解析；（3）819辆.

【解析】

（1）用每组中点值乘以频率，然后相加，得到平均值.（2）先用分层抽样的知识计算出量车中位于的车辆数，然后利用超几何分布的知识计算出分布列，并求得数学期望.（3）由（1）可知，计算出方差和标准差，利用正态分布的对称性，计算出在9:46～10:40这一时间段内通过的车辆的概率，乘以得到所求车辆数.

解：（1）这600辆车在9:20～10:40时间段内通过该收费点的时刻的平均值为，即10点04分。

（2）结合频率分布直方图和分层抽样的方法可知：抽取的10辆车中，在10:00前通过的车辆数就是位于时间分组中在这一区间内的车辆数，即，所以的可能取值为0，1，2，3，4。

所以，，，，，

所以的分布列为

	0	1	2	3	4

所以.

（3）由（1）可得，

，

所以.

估计在9:46～10:40这一时间段内通过的车辆数，也就是通过的车辆数，

由，得 ，

所以，估计在9:46～10:40这一时间段内通过的车辆数为（辆）.