
【题目】在平面直角坐标系xOy中,椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,右焦点为F,且椭圆E上的点到点F的距离的最小值为2.
,右焦点为F,且椭圆E上的点到点F的距离的最小值为2.
(1)求a,b的值;
(2)设椭圆E的左、右顶点分别为A,B,过点A的直线l与椭圆E及直线x=8分别相交于点M,N
①当过点A,F,N三点的圆半径最小时,求这个圆的方程;②若cos∠AMB= ![]() ,求△ABM的面积.
,求△ABM的面积.
【答案】
(1)解:由已知, ![]() =
= ![]() ,且a﹣c=2,
,且a﹣c=2,
解得a=4,c=2,
∴b2=a2﹣c2=12,
∴a=4,b=2 ![]() ;
;
(2)①由(1),A(﹣4,0),F(2,0),设N(8,t).
再设圆的方程为x2+y2+Dx+Ey+F=0,将点A,F,N的坐标代入,
得 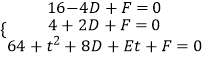 ,解得
,解得 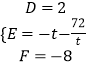 ,
,
∴圆的方程为x2+y2+2x﹣(t+ ![]() )y﹣8=0,
)y﹣8=0,
即(x+1)2+[y﹣ ![]() (t+
(t+ ![]() )]2=9+
)]2=9+ ![]() (t+
(t+ ![]() )2,
)2,
∵(t+ ![]() )2≥(2
)2≥(2 ![]() )2,当且仅当t+
)2,当且仅当t+ ![]() =±12
=±12 ![]() 时,圆的半径最小,
时,圆的半径最小,
故所求圆的方程为x2+y2+2x±12 ![]() y﹣8=0.
y﹣8=0.
②由对称性不妨设直线l的方程为y=k(x+4)(k>0).
由  ,得M(
,得M( ![]() ,
, ![]() ),
),
∴ ![]() =(
=( ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,
, ![]() ),
),
∴cos∠AMB= 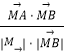 =
= ![]() =﹣
=﹣ ![]() ,
,
化简,得16k4﹣40k2﹣9=0,
解得k2= ![]() ,或k2=
,或k2= ![]() ,即k=
,即k= ![]() ,或k=
,或k= ![]() ,
,
此时总有yM=3.
∴△ABM的面积为 ![]() ×8×3=12.
×8×3=12.
【解析】1、本题考查的是由待定系数法求椭圆的方程。
2、(1)由已知条件,A(﹣4,0),F(2,0),设N(8,t).再设圆的方程为x2+y2+Dx+Ey+F=0,将点A,F,N的坐标代入得到圆的一般方程![]() ,把圆的方程整理基本不等式的形式求出最小值,当且仅当
,把圆的方程整理基本不等式的形式求出最小值,当且仅当![]() 圆的半径最小,故所求圆的方程为x2+y2+2x±12 2 y﹣8=0. (2)由对称性不妨设直线l的方程为y=k(x+4)(k>0)可得向量MA和MB的坐标表示,再由cos∠AMB的公式求得k的值,点M到直线的距离为3,所以三角形的面积为12.
圆的半径最小,故所求圆的方程为x2+y2+2x±12 2 y﹣8=0. (2)由对称性不妨设直线l的方程为y=k(x+4)(k>0)可得向量MA和MB的坐标表示,再由cos∠AMB的公式求得k的值,点M到直线的距离为3,所以三角形的面积为12.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(﹣1,0),B(1,1),C(2,0),点P是平面直角坐标系xOy上一点,且 ![]() =m
=m ![]() (m,n∈R),
(m,n∈R),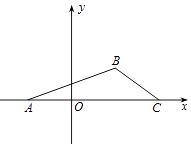
(1)若m=1,且 ![]() ∥
∥ ![]() ,试求实数n的值;
,试求实数n的值;
(2)若点P在△ABC三边围成的区域(含边界)上,求m+3n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(I)如果 ![]() 在
在 ![]() 处取得极值,求
处取得极值,求 ![]() 的值.
的值.
(II)求函数 ![]() 的单调区间.
的单调区间.
(III)当 ![]() 时,过点
时,过点 ![]() 存在函数曲线
存在函数曲线 ![]() 的切线,求
的切线,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在(1+x+x2)n= ![]() x
x ![]() x2+…
x2+… ![]() xr+…
xr+… ![]() x2n﹣1
x2n﹣1 ![]() x2n的展开式中,把D
x2n的展开式中,把D ![]() ,D
,D ![]() ,D
,D ![]() …,D
…,D ![]() …,D
…,D ![]() 叫做三项式系数
叫做三项式系数
(1)求D ![]() 的值
的值
(2)根据二项式定理,将等式(1+x)2n=(1+x)n(x+1)n的两边分别展开可得,左右两边xn的系数相等,即C ![]() =(C
=(C ![]() )2+(C
)2+(C ![]() )2+(C
)2+(C ![]() )2+…+(C
)2+…+(C ![]() )2 , 利用上述思想方法,请计算D
)2 , 利用上述思想方法,请计算D ![]() C
C ![]() ﹣D
﹣D ![]() C
C ![]() +D
+D ![]() C
C ![]() ﹣…+(﹣1)rD
﹣…+(﹣1)rD ![]() C
C ![]() +..
+.. ![]() C
C ![]() C
C ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将三颗骰子各掷一次,记事件A=“三个点数都不同”,B=“至少出现一个6点”,则条件概率P(A|B),P(B|A)分别是( )
A.![]() ,
, ![]()
B.![]() ,
, ![]()
C.![]() ,
, ![]()
D.![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得如表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(1+x)+alog2(1﹣x)(a∈R)的图象关于y轴对称.
(1)求函数f(x)的定义域;
(2)求a的值;
(3)若函数g(x)=x﹣2f(x)﹣2t有两个不同的零点,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,则该算法的功能是( ) 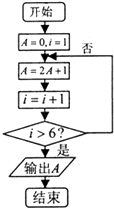
A.计算数列{2n﹣1}前5项的和
B.计算数列{2n﹣1}前5项的和
C.计算数列{2n﹣1}前6项的和
D.计算数列{2n﹣1}前6项的和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com