
| A. | $\frac{4}{5}$ | B. | $\frac{1}{10}$ | C. | $\frac{{3\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 已知ABC-A1B1C1是直三棱柱,取BC的中点0,连接A0,NM,BM,BM∥NO,BC∥NM,那么AN和NO所成角即为BM与AN所成角.求出边长,利用余弦定理求解角的大小.
解答 解:∵M,N分别是A1B1,A1C1的中点,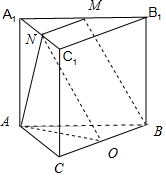
取BC的中点0,连接AO,NM,BM,
∴BM∥NO,BC∥NM且BC=2NM,
那么AN和NO所成角即为BM与AN所成角.
设BA=CA=CC1=2,∠BAC=90°,ABC-A1B1C1是直三棱柱,
∴AO=$\sqrt{2}$,AN=$\sqrt{5}$,BM=NO=$\sqrt{5}$,
∴cos∠ANO=$\frac{5+5-2}{2•\sqrt{5•\sqrt{5}}}$=$\frac{4}{5}$,
故选:A.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
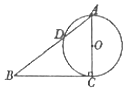 如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD( )cm.
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD( )cm.| A. | 5 | B. | $\frac{16}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{17}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,4] | B. | [2,+∞) | C. | (2,4) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,+∞) | C. | $({1,\root{4}{3}})$ | D. | $({\root{4}{3},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1365石 | B. | 338石 | C. | 168石 | D. | 134石 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com