
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线方程为y2=-4x,直线l的方程为2x+y-4=0,在抛物线上有一动点A,点A到y轴的距离为m,到直线l的距离为n,则m+n的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】启东市政府拟在蝶湖建一个旅游观光项目,设计方案如下:如图所示的圆O是圆形湖的边界,沿线段AB,BC,CD,DA建一个观景长廊,其中A,B,C,D是观景长廊的四个出入口且都在圆O上,已知:BC=12百米,AB=8百米,在湖中P处和湖边D处各建一个观景亭,且它们关于直线AC对称,在湖面建一条观景桥APC.观景亭的大小、观景长廊、观景桥的宽度均忽略不计,设![]() .
.
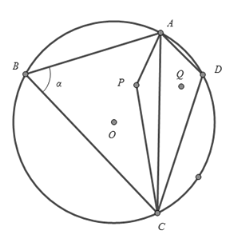
(1)若观景长廊AD=4百米,CD=AB,求由观景长廊所围成的四边形ABCD内的湖面面积;
(2)当![]() 时,求三角形区域ADC内的湖面面积的最大值;
时,求三角形区域ADC内的湖面面积的最大值;
(3)若CD=8百米且规划建亭点P在三角形ABC区域内(不包括边界),试判断四边形ABCP内湖面面积是否有最大值?若有,求出最大值,并写出此时![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一(1)班参加校生物竞赛学生的成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:

(1)求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在[80,100]之间的学生中任选2人进行某项研究,求至少有1人分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆C:
中,椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,P为椭圆C上一点,且
,P为椭圆C上一点,且![]() 垂直于
垂直于![]() 轴,连结
轴,连结![]() 并延长交椭圆于另一点
并延长交椭圆于另一点![]() ,设
,设![]()
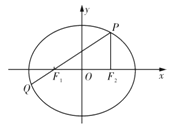
(1)若点![]() 的坐标为
的坐标为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)若![]() ,求椭圆
,求椭圆![]() 的离心率的取值范围
的离心率的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年“中秋节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(![]() )分成七段
)分成七段![]() 后得到如图所示的频率分布直方图,据图解答下列问题:
后得到如图所示的频率分布直方图,据图解答下列问题:
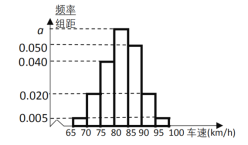
(1)求![]() 的值,并说明交警部门采用的是什么抽样方法?
的值,并说明交警部门采用的是什么抽样方法?
(2)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1);
(3)若该路段的车速达到或超过![]() 即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com