
【题目】如图,在三棱台ABO﹣A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1 , OB=3,O1B1=1,OO1= ![]() .
. 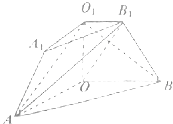
(1)证明:AB1⊥BO1;
(2)求直线AO1与平面AOB1所成的角的正切值;
(3)求二面角O﹣AB1﹣O1的余弦值.
【答案】
(1)证明:由题设知OA⊥OO1,且平面AOO1A1⊥平面OBB1O1,
平面AOO1A1∩平面OBB1O1=OO1,
则OA⊥平面OBB1O1,所以OA⊥OB,OA⊥BO1,
又因为 ![]() .O1B1=1,OB=3,
.O1B1=1,OB=3,
所以∠OO1B=60°,∠O1OB1=30°,
从而OB1⊥BO1,又因为OA⊥BO1,OB1∩OA=O,
故BO1⊥平面AOB1,又AB1平面AOB1,故AB1⊥BO1
(2)解:以O为原点,OA、OB、OO1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
如图,则A(3,0,0),B(0,3,0),B1(0,1, ![]() ),O1(0,0,
),O1(0,0, ![]() ).
).
由(1)知BO1⊥平面OA B1,从而 ![]() 是平面OA B1的一个法向量.
是平面OA B1的一个法向量.
![]() ,
, ![]() ,
,
设直线AO1与平面AOB1所成的角为α,
![]() .cosα=
.cosα= ![]() =
= ![]() ,
,
tanα= ![]() =
= ![]() .
.
∴直线AO1与平面AOB1所成的角的正切值为 ![]()
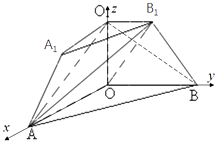
(3)解:由(II)知 ![]() 是平面OA B1的一个法向量.且
是平面OA B1的一个法向量.且 ![]() ,
,
设 ![]() 是平面O1A B1的一个法向量,
是平面O1A B1的一个法向量,
由  ,得
,得 ![]() .
.
设二面角O﹣AB1﹣O1的大小为,
则cosθ=cos<, ![]() >=
>=
即二面角O﹣AB1﹣O1的余弦值是 ![]()
【解析】(1)推导出OA⊥OB,OA⊥BO1 , OB1⊥BO1 , OA⊥BO1
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则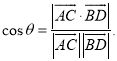 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了各个城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调研机构在该市随机抽取了
市的使用情况,某调研机构在该市随机抽取了![]() 位市民进行调查,得到的
位市民进行调查,得到的![]() 列联表如下:
列联表如下:
经常使用 | 偶尔或不用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)根据以上数据,能否在犯错误的概率不超过![]() 的前提下认为使用共享单车的情况与年龄有关?
的前提下认为使用共享单车的情况与年龄有关?
(2)现从所抽取的![]() 岁以上的市民中利用分层抽样的方法再抽取
岁以上的市民中利用分层抽样的方法再抽取![]() 位市民,从这
位市民,从这![]() 位市民中随机选出
位市民中随机选出![]() 位市民赠送礼品,求选出的
位市民赠送礼品,求选出的![]() 位市民中至少有
位市民中至少有![]() 位市民经常使用共享单车的概率.
位市民经常使用共享单车的概率.
参考公式及数据:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项都大于1,且a1=2,a ![]() ﹣an+1﹣a
﹣an+1﹣a ![]() +1=0(n∈N*).
+1=0(n∈N*).
(1)求证: ![]() ≤an<an+1≤n+2;
≤an<an+1≤n+2;
(2)求证: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <1.
<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项都大于1,且a1=2,a ![]() ﹣an+1﹣a
﹣an+1﹣a ![]() +1=0(n∈N*).
+1=0(n∈N*).
(1)求证: ![]() ≤an<an+1≤n+2;
≤an<an+1≤n+2;
(2)求证: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <1.
<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2016年“猴”年的到来,某电视台举办猜奖活动,参与者需先后回答两道选择题,问题A有三个选项,问题B有四个选项,每题只有一个选项是正确的,正确回答问题A可获奖金1千元,正确回答问题B可获奖金2千元.活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止.假设某参与者在回答问题前,选择每道题的每个选项的机会是等可能的.
(Ⅰ)如果该参与者先回答问题A,求其恰好获得奖金1千元的概率;
(Ⅱ)试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知存在常数![]() ,那么函数
,那么函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,再由函数的奇偶性可知在
上是增函数,再由函数的奇偶性可知在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
(1)判断函数![]() 的单调性,并证明:
的单调性,并证明:
(2)将前述的函数![]() 和
和![]() 推广为更为一般形式的函数
推广为更为一般形式的函数![]() ,使
,使![]() 和
和![]() 都是
都是![]() 的特例,研究
的特例,研究![]() 的单调性(只须归纳出结论,不必推理证明)
的单调性(只须归纳出结论,不必推理证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班从6名班干部(其中男生4人,女生2人)中选3人参加学校学生会的干部
竞选.
(Ⅰ)设所选3人中女生人数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)在男生甲被选中的情况下,求女生乙也被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,命题p:x∈[-2,-1],x2-a≥0,命题q:![]() .
.
(1)若命题p为真命题,求实数a的取值范围;
(2)若命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
(Ⅰ)若BM=2MP,求证:PD∥平面MAC;
(Ⅱ)若平面PAB⊥平面ABCD,平面PAD⊥平面ABCD,求证:PA⊥平面ABCD;
(Ⅲ)在(Ⅱ)的条件下,若二面角B﹣AC﹣M的余弦值为 ![]() ,求
,求 ![]() 的值.
的值.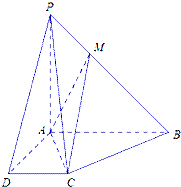
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com