
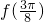 .
.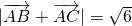 ,求△ABC的面积.
,求△ABC的面积.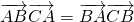
 |•|
|•| |cos(π-A)=|
|cos(π-A)=| |•|
|•| |cos(π-B)
|cos(π-B) |cosA=|
|cosA=| |cosB,即bcosA=acosB
|cosB,即bcosA=acosB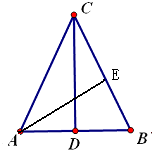
 =-|
=-| |•|
|•| |cosA=-1
|cosA=-1 |•|
|•| |•
|•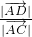 =-1,得-
=-1,得- |
| |2=-1
|2=-1 |2=2,得|
|2=2,得| |=
|= ,即AB边的长为
,即AB边的长为 ;
;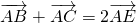 ,
,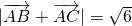 ,∴|
,∴| |=
|=
 ,可得△ABC是边长等于
,可得△ABC是边长等于 的等边三角形,
的等边三角形, ×(
×( )2=
)2= .
. |cosA=|
|cosA=| |cosB,结合正弦定理得sin(A-B)=0,从而得到A=B,得△ABC是以AB为底边的等腰三角形;
|cosB,结合正弦定理得sin(A-B)=0,从而得到A=B,得△ABC是以AB为底边的等腰三角形; =-1化简可得-
=-1化简可得- |
| |2=-1,从而算出|
|2=-1,从而算出| |=
|= ,得到AB边的长;
,得到AB边的长; ,设AC=BC=x,利用三角形中线满足的平方关系列式,得6+x2=2(x2+2),解得x=
,设AC=BC=x,利用三角形中线满足的平方关系列式,得6+x2=2(x2+2),解得x= ,得△ABC是边长等于
,得△ABC是边长等于 的等边三角形,从而得到△ABC的面积S=
的等边三角形,从而得到△ABC的面积S= .
.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com