
如图所示,在圆锥PO中, PO=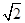 ,ʘO的直径AB=2, C为弧AB的中点,D为AC的中点.
,ʘO的直径AB=2, C为弧AB的中点,D为AC的中点.

(1)求证:平面POD^平面PAC;
(2)求二面角B—PA—C的余弦值.
(1)见解析;(2)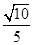
【解析】
试题分析:(1)通过证平面PAC内直线AC^平面POD,由平面与平面垂直的判定定理得平面PAC^平面POD;(2)用垂面法作出二面角的平面角,然后在直角三角形中利用边长求平面角的余弦值.
试题解析:证明:(1)如图所示,连接OC.
 OA=OC,D是AC的中点,\AC^OD,在圆锥PO中,PA=PC,
OA=OC,D是AC的中点,\AC^OD,在圆锥PO中,PA=PC,
则AC^PD,又PDÇOD=D,\AC^平面POD,而ACÌ平面PAC,
\平面POD^平面PAC 5分
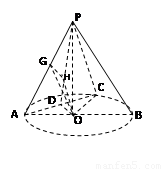
(2)在平面POD中,过O作OH^PD于H,由(1)知:
平面POD^平面PAC,\OH^平面PAC,过H作HG^PA于G,连OG,则OG^PA(三垂线定理)
\ÐOGH为二面角B—PA—C的平面角,
在RtDODA中,OD=OA×450=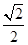 .
.
在RtDPOD中,OH= 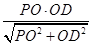 =
=
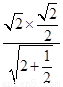 =
=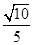 .
.
在RtDPOA中,OG= 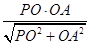 =
=
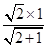 =
=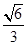 .
.
在RtDOHG中,sinÐOGH= 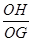 =
=
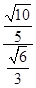 =
=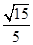 .
.
所以,cosÐOGH= 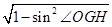 =
=
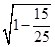 =
=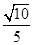
所以,二面角B—PA—C的余弦值为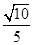 .
10分
.
10分
考点:1.平面与平面垂直的判定;2.二面角的平面角作法与求法


科目:高中数学 来源:2012年江苏省南京市白下区高三迎市二模考试数学试卷(解析版) 题型:解答题
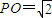 ,⊙O的直径AB=2,点C在弧AB上,且∠COB=60°,则二面角B-PA-C的余弦值是 .
,⊙O的直径AB=2,点C在弧AB上,且∠COB=60°,则二面角B-PA-C的余弦值是 .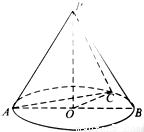
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com