
ЎҫМвДҝЎҝДіЖыіөЖ·ЕЖОӘБЛБЛҪвҝН»§¶ФУЪЖдЖмПВөДОеЦЦРНәЕЖыіөөДВъТвЗйҝцЈ¬Лж»ъійИЎБЛТ»Р©ҝН»§ҪшРР»Ш·ГЈ¬өчІйҪб№ыИзПВұнЈә
ЖыіөРНәЕ | I | II | III | IV | V |
»Ш·ГҝН»§ЈЁИЛКэЈ© | 250 | 100 | 200 | 700 | 350 |
ВъТвВК | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
ВъТвВККЗЦёЈәДіЦЦРНәЕЖыіөөД»Ш·ГҝН»§ЦРЈ¬ВъТвИЛКэУлЧЬИЛКэөДұИЦө.
јЩЙиҝН»§КЗ·сВъТв»ҘПа¶АБўЈ¬ЗТГҝЦЦРНәЕЖыіөҝН»§¶ФУЪҙЛРНәЕЖыіөВъТвөДёЕВКУлұнёсЦРёГРНәЕЖыіөөДВъТвВКПаөИ.
(1)ҙУЛщУРөД»Ш·ГҝН»§ЦРЛж»ъійИЎ1ИЛЈ¬ЗуХвёцҝН»§ВъТвөДёЕВКЈ»
(2)ҙУIРНәЕәНVРНәЕЖыіөөДЛщУРҝН»§ЦРёчЛж»ъійИЎ1ИЛЈ¬ЙиЖдЦРВъТвөДИЛКэОӘ![]() Ј¬Зу
Ј¬Зу![]() өД·ЦІјБРәНЖЪНыЈ»
өД·ЦІјБРәНЖЪНыЈ»
(3)УГ Ў°![]() Ўұ, Ў°
Ўұ, Ў°![]() Ўұ, Ў°
Ўұ, Ў°![]() Ўұ, Ў°
Ўұ, Ў°![]() Ўұ, Ў°
Ўұ, Ў°![]() Ўұ·ЦұрұнКҫI, II, III, IV, VРНәЕЖыіөИГҝН»§ВъТвЈ¬ Ў°
Ўұ·ЦұрұнКҫI, II, III, IV, VРНәЕЖыіөИГҝН»§ВъТвЈ¬ Ў°![]() Ўұ, Ў°
Ўұ, Ў°![]() Ўұ, Ў°
Ўұ, Ў°![]() Ўұ, Ў°
Ўұ, Ў°![]() Ўұ, Ў°
Ўұ, Ў°![]() Ўұ ·ЦұрұнКҫI, II, III, IV, VРНәЕЖыіөИГҝН»§І»ВъТв.Рҙіц·ҪІо
Ўұ ·ЦұрұнКҫI, II, III, IV, VРНәЕЖыіөИГҝН»§І»ВъТв.Рҙіц·ҪІо![]() өДҙуРЎ№ШПө.
өДҙуРЎ№ШПө.
Ўҫҙр°ёЎҝ(1) ![]() (2)јыҪвОцЈ»(3)
(2)јыҪвОцЈ»(3)![]()
ЎҫҪвОцЎҝ
ЈЁ1Ј©ЗуіцСщұҫЦРөД»Ш·ГҝН»§өДЧЬКэәНВъТвөДҝН»§ИЛКэЈ¬јҙҝЙЗуіцёЕВКЈ»
ЈЁ2Ј©УЙМвЗуіцВъТвөДИЛКэОӘ![]() өД·ЦІјБРЈ¬јМ¶шЗуіцЖЪНы;
өД·ЦІјБРЈ¬јМ¶шЗуіцЖЪНы;
ЈЁ3Ј©ёщҫЭ№«КҪЦұҪУөГіцҪб№ыЈ¬И»әуЧчұИҪП.
ЈЁ1Ј©УЙМвТвЦӘЈ¬СщұҫЦРөД»Ш·ГҝН»§өДЧЬКэКЗ![]() Ј¬
Ј¬
ВъТвөДҝН»§ИЛКэ![]() Ј¬
Ј¬
№КЛщЗуёЕВКОӘ![]() Ј®
Ј®
ЈЁ2Ј©![]() .
.
ЙиКВјю![]() ОӘЎ°ҙУIРНәЕЖыіөЛщУРҝН»§ЦРЛж»ъійИЎөДИЛВъТвЎұЈ¬
ОӘЎ°ҙУIРНәЕЖыіөЛщУРҝН»§ЦРЛж»ъійИЎөДИЛВъТвЎұЈ¬
КВјю![]() ОӘЎ°ҙУVРНәЕЖыіөЛщУРҝН»§ЦРЛж»ъійИЎөДИЛВъТвЎұЈ¬ЗТ
ОӘЎ°ҙУVРНәЕЖыіөЛщУРҝН»§ЦРЛж»ъійИЎөДИЛВъТвЎұЈ¬ЗТ![]() Ўў
Ўў![]() ОӘ¶АБўКВјю.
ОӘ¶АБўКВјю.
ёщҫЭМвТвЈ¬![]() №АјЖОӘ0.5Ј¬
№АјЖОӘ0.5Ј¬![]() №АјЖОӘ0.2 .
№АјЖОӘ0.2 .
Фт![]() ;
;
![]()
![]() ;
;
![]() .
.
![]() өД·ЦІјБРОӘ
өД·ЦІјБРОӘ
|
|
|
|
|
|
|
|
![]() өДЖЪНы
өДЖЪНы![]()
ЈЁ3Ј©УЙМвЈ¬IРНәЕөДЖҪҫщКэОӘ0.5,ЛщТФ![]() =
=![]()
Н¬Ан![]() =
=![]()
Н¬Ан![]() =0.24Ј»
=0.24Ј»![]() =0.21Ј»
=0.21Ј»![]() =0.16
=0.16
ЛщТФ![]() Ј®
Ј®


 МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё
МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіРЈёЯИэЈЁ1Ј©°аФЪТ»ҙОУпОДІвКФҪбКшәуЈ¬·ўПЦН¬С§ГЗФЪұіЛРДЪИЭ·ҪГжК§·ЦҪПОӘСПЦШ.ОӘБЛМбЙэұіЛРР§№ыЈ¬°аЦчИОі«ТйҙујТФЪФз•Ҡ¶БКұјдХҫЖрАҙҙуЙщЛР¶БЈ¬ОӘБЛҪвН¬С§ГЗ¶ФХҫЖрАҙҙуЙщЛР¶БөДМ¬¶ИЈ¬¶ФИ«°а50ГыН¬С§ҪшРРөчІйЈ¬Ҫ«өчІйҪб№ыҪшРРХыАнәуЦЖіЙИзұнЈә
ҝјКФ·ЦКэ |
|
|
|
|
|
|
ЖөКэ | 5 | 10 | 15 | 5 | 10 | 5 |
ФЮіЙИЛКэ | 4 | 6 | 9 | 3 | 6 | 4 |
ЈЁ1Ј©УыК№ІвКФУЕРгВКОӘ![]() Ј¬ФтУЕРг·ЦКэПЯУҰ¶ЁОӘ¶аЙЩ·ЦЈҝ
Ј¬ФтУЕРг·ЦКэПЯУҰ¶ЁОӘ¶аЙЩ·ЦЈҝ
ЈЁ2Ј©ТАҫЭөЪ1ОКөДҪб№ыј°СщұҫКэҫЭСРҫҝКЗ·сФЮіЙХҫЖрАҙҙуЙщЛР¶БөДМ¬¶ИУлҝјКФіЙјЁКЗ·сУЕРгөД№ШПөЈ¬БРіц2ЎБ2БРБӘұнЈ¬ІўЕР¶ПКЗ·сУР![]() өД°СОХИПОӘФЮіЙУл·сөДМ¬¶ИУліЙјЁКЗ·сУЕРгУР№ШПө.
өД°СОХИПОӘФЮіЙУл·сөДМ¬¶ИУліЙјЁКЗ·сУЕРгУР№ШПө.
ІОҝј№«КҪј°КэҫЭЈә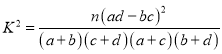 Ј¬
Ј¬![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() ФЪ
ФЪ![]() ҙҰИЎөГј«ЦөAЈ¬әҜКэ
ҙҰИЎөГј«ЦөAЈ¬әҜКэ![]() Ј¬ЖдЦР
Ј¬ЖдЦР![]() ЎӯКЗЧФИ»¶ФКэөДөЧКэЈ®
ЎӯКЗЧФИ»¶ФКэөДөЧКэЈ®
ЈЁ1Ј©ЗуmөДЦөЈ¬ІўЕР¶ПAКЗ![]() өДЧоҙуЦө»№КЗЧоРЎЦөЈ»
өДЧоҙуЦө»№КЗЧоРЎЦөЈ»
ЈЁ2Ј©Зу![]() өДөҘөчЗшјдЈ»
өДөҘөчЗшјдЈ»
ЈЁ3Ј©ЦӨГчЈә¶ФУЪИОТвХэХыКэnЈ¬І»өИКҪ![]() іЙБўЈ®
іЙБўЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘКэБР{an}өДЗ°nПоәНSnәННЁПоanВъЧг![]() .
.
ЈЁ1Ј©ЗуКэБР{an}өДНЁПКҪЈ»
ЈЁ2Ј©өИІоКэБР{bn}ЦРЈ¬b1ЈҪ3a1Ј¬b2ЈҪ2Ј¬ЗуКэБР{an+bn}өДЗ°nПоәНTn.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј®
Ј®
ЈЁ1Ј©ЗуәҜКэ![]() өДј«ЦөЈ»
өДј«ЦөЈ»
ЈЁ2Ј©ЦұПЯ![]() ОӘәҜКэ
ОӘәҜКэ![]() НјПуөДТ»МхЗРПЯЈ¬Иф¶ФИОТвөД
НјПуөДТ»МхЗРПЯЈ¬Иф¶ФИОТвөД![]() Ј¬
Ј¬![]() ¶јУР
¶јУР![]() іЙБўЈ¬ЗуКөКэ
іЙБўЈ¬ЗуКөКэ![]() өДИЎЦө·¶О§Ј®
өДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЛДАвЧ¶P©ҒABCDЦРЈ¬ЖҪГжABCDЎНЖҪГжPADЈ¬ADЎОBCЈ¬ABЈҪBC![]() ADЈҪ1Ј¬ЎПAPDЈҪЎПBADЈҪ90Ўг.
ADЈҪ1Ј¬ЎПAPDЈҪЎПBADЈҪ90Ўг.
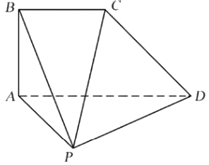
ЈЁ1Ј©ЗуЦӨЈәPDЎНPBЈ»
ЈЁ2Ј©өұPAЈҪPDКұЈ¬ЗуИэАвЧ¶P©ҒBCDөДМе»э.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэfЈЁxЈ©![]() ЈЁcosҰИ+1Ј©cos2x+cosҰИЈЁcosx+1Ј©Ј¬УРПВКцЛДёцҪбВЫЈәўЩfЈЁxЈ©КЗЕјәҜКэЈ»ўЪfЈЁxЈ©ФЪЈЁ
ЈЁcosҰИ+1Ј©cos2x+cosҰИЈЁcosx+1Ј©Ј¬УРПВКцЛДёцҪбВЫЈәўЩfЈЁxЈ©КЗЕјәҜКэЈ»ўЪfЈЁxЈ©ФЪЈЁ![]() Ј¬
Ј¬![]() Ј©ЙПөҘөчөЭјхЈ»ўЫөұҰИЎК[
Ј©ЙПөҘөчөЭјхЈ»ўЫөұҰИЎК[![]() Ј¬
Ј¬![]() ]КұЈ¬УР|fЈЁxЈ©|
]КұЈ¬УР|fЈЁxЈ©|![]() Ј»ўЬөұҰИЎК[
Ј»ўЬөұҰИЎК[![]() Ј¬
Ј¬![]() ]КұЈ¬УР|f'ЈЁxЈ©|
]КұЈ¬УР|f'ЈЁxЈ©|![]() Ј»ЖдЦРЛщУРХжГьМвөДұаәЕКЗ( )
Ј»ЖдЦРЛщУРХжГьМвөДұаәЕКЗ( )
A.ўЩўЫB.ўЪўЬC.ўЩўЫўЬD.ўЩўЬ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ![]() КЗЕЧОпПЯ
КЗЕЧОпПЯ![]() ЙПО»УЪ
ЙПО»УЪ![]() ЦбБҪІаөДІ»Н¬БҪөг
ЦбБҪІаөДІ»Н¬БҪөг
ЈЁ1Ј©Иф![]() ФЪЦұПЯ
ФЪЦұПЯ![]() ЙПЈ¬ЗТК№өГТФ
ЙПЈ¬ЗТК№өГТФ![]() ОӘ¶ҘөгөДЛДұЯРОЗЎОӘХэ·ҪРОЈ¬ЗуёГХэ·ҪРОөДГж»э.
ОӘ¶ҘөгөДЛДұЯРОЗЎОӘХэ·ҪРОЈ¬ЗуёГХэ·ҪРОөДГж»э.
ЈЁ2Ј©Зу№э![]() Ўў
Ўў![]() өДЗРПЯУлЦұПЯ
өДЗРПЯУлЦұПЯ![]() О§іЙөДИэҪЗРОГж»эөДЧоРЎЦөЈ»
О§іЙөДИэҪЗРОГж»эөДЧоРЎЦөЈ»
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝУРТ»ёцН¬С§јТҝӘБЛТ»ёцРЎВфІҝЈ¬ЛыОӘБЛСРҫҝЖшОВ¶ФИИТыТыБППъКЫөДУ°ПмЈ¬ҫӯ№эНіјЖЈ¬өГөҪТ»ёцВфіцөДИИТыұӯКэУлөұМмЖшОВөДЙўөгНјәН¶ФұИұнЈә
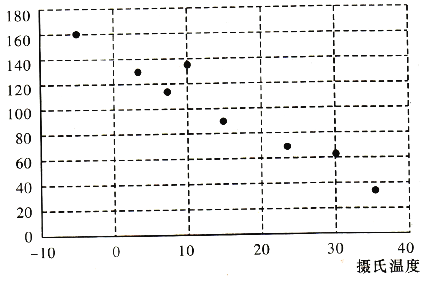
ЙгКПОВ¶И |
|
|
|
|
|
|
|
|
ИИТыұӯКэ |
|
|
|
|
|
|
|
|
ЈЁ1Ј©ҙУЙўөгНјҝЙТФ·ўПЦЈ¬ёчөгЙўІјФЪҙУЧуЙПҪЗөҪУТПВҪЗөДЗшУтАпЎЈТтҙЛЈ¬ЖшОВУлөұМмИИТыПъКЫұӯКэЦ®јдіЙёәПа№ШЈ¬јҙЖшОВФҪёЯЈ¬өұМмВфіцИҘөДИИТыұӯКэФҪЙЩЎЈНіјЖЦРіЈУГПа№ШПөКэ![]() АҙәвБҝБҪёцұдБҝЦ®јдПЯРФ№ШПөөДЗҝИх.НіјЖС§ИПОӘЈ¬¶ФУЪұдБҝ
АҙәвБҝБҪёцұдБҝЦ®јдПЯРФ№ШПөөДЗҝИх.НіјЖС§ИПОӘЈ¬¶ФУЪұдБҝ![]() Ўў
Ўў![]() Ј¬Из№ы
Ј¬Из№ы![]() Ј¬ДЗГҙёәПа№ШәЬЗҝЈ»Из№ы
Ј¬ДЗГҙёәПа№ШәЬЗҝЈ»Из№ы![]() Ј¬ДЗГҙХэПа№ШәЬЗҝЈ»Из№ы
Ј¬ДЗГҙХэПа№ШәЬЗҝЈ»Из№ы![]() Ј¬ДЗГҙПа№ШРФТ»°гЈ»Из№ы
Ј¬ДЗГҙПа№ШРФТ»°гЈ»Из№ы![]() Ј¬ДЗГҙПа№ШРФҪПИхЎЈЗлёщҫЭТСЦӘКэҫЭЈ¬ЕР¶ПЖшОВУлөұМмИИТыПъКЫұӯКэПа№ШРФөДЗҝИх.
Ј¬ДЗГҙПа№ШРФҪПИхЎЈЗлёщҫЭТСЦӘКэҫЭЈ¬ЕР¶ПЖшОВУлөұМмИИТыПъКЫұӯКэПа№ШРФөДЗҝИх.
ЈЁ2Ј©ЈЁiЈ©ЗлёщҫЭТСЦӘКэҫЭЗуіцЖшОВУлөұМмИИТыПъКЫұӯКэөДПЯРФ»Ш№й·ҪіМЈ»
ЈЁiiЈ©јЗ![]() ОӘІ»і¬№э
ОӘІ»і¬№э![]() өДЧоҙуХыКэЈ¬Из
өДЧоҙуХыКэЈ¬Из![]() Ј¬
Ј¬![]() .¶ФУЪЈЁiЈ©ЦРЗуіцөДПЯРФ»Ш№й·ҪіМ
.¶ФУЪЈЁiЈ©ЦРЗуіцөДПЯРФ»Ш№й·ҪіМ![]() Ј¬Ҫ«
Ј¬Ҫ«![]() КУОӘЖшОВУлөұМмИИТыПъКЫұӯКэөДәҜКэ№ШПө.ТСЦӘЖшОВ
КУОӘЖшОВУлөұМмИИТыПъКЫұӯКэөДәҜКэ№ШПө.ТСЦӘЖшОВ![]() УлөұМмИИТыГҝұӯөДПъКЫАыИу
УлөұМмИИТыГҝұӯөДПъКЫАыИу![]() өД№ШПөКЗ
өД№ШПөКЗ![]()
![]() ЈЁөҘО»ЈәФӘЈ©Ј¬ЗлОКөұЖшОВ
ЈЁөҘО»ЈәФӘЈ©Ј¬ЗлОКөұЖшОВ![]() ОӘ¶аЙЩКұЈ¬өұМмөДИИТыПъКЫАыИуЧЬ¶оЧоҙуЈҝ
ОӘ¶аЙЩКұЈ¬өұМмөДИИТыПъКЫАыИуЧЬ¶оЧоҙуЈҝ
ЈЁІОҝј№«КҪЈ©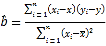 Ј¬
Ј¬![]() Ј¬
Ј¬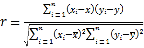
ЈЁІОҝјКэҫЭЈ©![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
![]() .
.
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com