练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，已知a=bcosC+csinB，b=2，则△ABC面积的最大值为 ．

    【答案】 +1
    【解析】解：在△ABC中，∵a=bcosC+ccosB，又a=bcosC+csinB，b=2，
    ∴cosB=sinB，
    ∴tanB=1，B∈（0，π）．
    由余弦定理可得：b2=a2+c2﹣2accosB，
    ∴4≥2ac﹣ ac，当且仅当a=c时取等号．
    ∴ac≤4+2 ．
    ∴S△ABC= acsinB≤ （4+2 ）× = +1．
    故答案为： +1．
    a=bcosC+ccosB，又a=2cosC+csinB，b=2，可得B．由余弦定理可得：b2=a2+c2﹣2accosB，利用基本不等式的性质可得ac≤4+2 ，即可得出三角形面积的最大值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，椭圆E： =1（a＞b＞0）的焦距为2，且过点（ ， ）．
    （1）求椭圆E的方程；
    （2）若点A，B分别是椭圆E的左、右顶点，直线l经过点B且垂直于x轴，点P是椭圆上异于A，B的任意一点，直线AP交l于点M． ①设直线OM的斜率为k1 ， 直线BP的斜率为k2 ， 求证：k1k2为定值；
    ②设过点M垂直于PB的直线为m．求证：直线m过定点，并求出定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AB⊥AD，AD∥BC，AD= BC=2，E在BC上，且BE= AB=1，侧棱PA⊥平面ABCD．
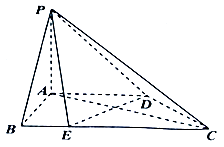
    （1）求证：平面PDE⊥平面PAC；
    （2）若△PAB为等腰直角三角形． （i）求直线PE与平面PAC所成角的正弦值；
    （ii）求二面角A﹣PC﹣D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在R上的函数f（x）满足2f（4﹣x）=f（x）+x2﹣2，则曲线y=f（x）在点（2，f（2））处的切线方程是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 ，函数 ，若函数f（x）图象的两个相邻的对称轴间的距离为 ．
    （1）求函数f（x）的单调增区间；
    （2）在△ABC中，角A，B，C所对的边分别是a，b，c，若△ABC满足f（A）=1，a=3，BC边上的中线长为3，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|2x﹣1|+|2x+a|，g（x）=x+3．
    （1）当a=2时，求不等式f（x）＜g（x）的解集；
    （2）设a＞ ，且当x∈[ ，a]时，f（x）≤g（x），求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面内将点A（2，1）绕原点按逆时针方向旋转 ，得到点B，则点B的坐标为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-5：不等式选讲]

    已知函数f（x）=|ax﹣2|．
    （Ⅰ）当a=2时，解不等式f（x）＞x+1；
    （Ⅱ）若关于x的不等式f（x）+f（﹣x）＜ 有实数解，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】据某市地产数据研究院的数据显示，2016年该市新建住宅销售均价走势如图所示，为抑制房价过快上涨，政府从8月份采取宏观调控措施，10月份开始房价得到很好的抑制．

    （Ⅰ）地产数据研究院研究发现，3月至7月的各月均价y（万元/平方米）与月份x之间具有较强的线性相关关系，试建立y关于x的回归方程（系数精确到0.01），政府若不调控，依次相关关系预测第12月份该市新建住宅销售均价；
    （Ⅱ）地产数据研究院在2016年的12个月份中，随机抽取三个月份的数据作样本分析，若关注所抽三个月份的所属季度，记不同季度的个数为X，求X的分布列和数学期望．
    参考数据： =25， =5.36， =0.64
    回归方程 中斜率和截距的最小二乘估计公式分别为：
    = ， ．

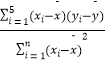    查看答案和解析>>

    同步练习册答案