
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 分别为
分别为![]() 与
与![]() 轴,
轴, ![]() 轴的交点.
轴的交点.
(1)写出![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 的极坐标;
的极坐标;
(2)设![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的极坐标方程.
的极坐标方程.
 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一条对称轴为
的一条对称轴为![]() ,且最高点的纵坐标是
,且最高点的纵坐标是![]() .
.
(1)求![]() 的最小值及此时函数
的最小值及此时函数![]() 的最小正周期、初相;
的最小正周期、初相;
(2)在(1)的情况下,设![]() ,求函数
,求函数![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办“中国诗词大赛”活动,某班派出甲乙两名选手同时参加比赛. 大赛设有15个诗词填空题,其中“唐诗”、“宋词”和“毛泽东诗词”各5个.每位选手从三类诗词中各任选1个进行作答,3个全答对选手得3分,答对2个选手得2分,答对1个选手得1分,一个都没答对选手得0分. 已知“唐诗”、“宋词”和“毛泽东诗词”中甲能答对的题目个数依次为5,4,3,乙能答对的题目个数依此为4,5,4,假设每人各题答对与否互不影响,甲乙两人答对与否也互不影响.
求:(1)甲乙两人同时得到3分的概率;
(2)甲乙两人得分之和![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() 为参数). 点
为参数). 点![]() 是曲线
是曲线![]() 上两点,点
上两点,点![]() 的极坐标分别为
的极坐标分别为![]() .
.
(1)写出曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线
上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线![]() ,又已知直线
,又已知直线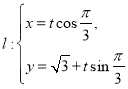 (
(![]() 是参数),且直线
是参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(I)求曲线![]() 的直角坐标方程,并说明它是什么曲线;
的直角坐标方程,并说明它是什么曲线;
(II)设定点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有穷数列![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,若数列
,若数列![]() 中各项都是集合
中各项都是集合![]() 的元素,则称该数列为
的元素,则称该数列为![]() 数列.
数列.
对于![]() 数列
数列![]() ,定义如下操作过程
,定义如下操作过程![]() 从
从![]() 中任取两项
中任取两项![]() ,
, ![]() ,将
,将![]() 的值添在
的值添在![]() 的最后,然后删除
的最后,然后删除![]() ,
, ![]() ,这样得到一个
,这样得到一个![]() 项的新数列,记作
项的新数列,记作![]() (约定:一个数也视作数列).若
(约定:一个数也视作数列).若![]() 还是
还是![]() 数列,可继续实施操作过程
数列,可继续实施操作过程![]() .得到的新数列记作
.得到的新数列记作![]() ,
, ![]() ,如此经过
,如此经过![]() 次操作后得到的新数列记作
次操作后得到的新数列记作![]() .
.
(Ⅰ)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,请写出
,请写出![]() 的所有可能的结果.
的所有可能的结果.
(Ⅱ)求证:对![]() 数列
数列![]() 实施操作过程
实施操作过程![]() 后得到的数列
后得到的数列![]() 仍是
仍是![]() 数列.
数列.
(Ⅲ)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的所有可能的结果,并说明理由.
的所有可能的结果,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com