
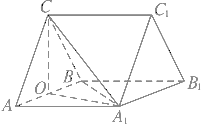
【题目】如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
O为AB的中点
(1)证明:AB⊥平面A1OC
(2)若AB=CB=2,平面ABC![]() 平面A1ABB1,求三棱柱ABC-A1B1C1的体积.
平面A1ABB1,求三棱柱ABC-A1B1C1的体积.
【答案】(1)见解析;(2)3
【解析】
(1)利用有一个角是![]() 的等腰三角形是等边三角形,证得三角形
的等腰三角形是等边三角形,证得三角形![]() 是等边三角形,由此证得
是等边三角形,由此证得![]() ,再根据三角形
,再根据三角形![]() 为等腰三角形证得
为等腰三角形证得![]() ,故
,故![]() 平面
平面![]() .(2)由(1)利用面面垂直的性质定理,证得
.(2)由(1)利用面面垂直的性质定理,证得![]() 平面
平面![]() ,即
,即![]() 为三棱柱的高,由此可求得三棱柱的体积.
为三棱柱的高,由此可求得三棱柱的体积.
(1)证明:连结A1B.,因为CA=CB,OA=OB,所OC⊥AB

因为AB=AA1,∠BAA1=60°,所三角形AA1B为等边三角形,
所以AA1=A1B,又OA=OB,所以OA1⊥AB,又![]() =
=![]() ,
,![]() 面A1OC
面A1OC
(2)由题可知,![]() 与
与![]() 是边长为2的等边三角形,得
是边长为2的等边三角形,得![]()
![]() 平面ABC
平面ABC![]() 平面A1ABB 平面ABC
平面A1ABB 平面ABC![]() 平面A1ABB=AB,
平面A1ABB=AB,
由(1)OA1⊥AB,![]() 平面A1ABB
平面A1ABB
![]() 面ABC
面ABC
![]() 为三棱柱ABC-A1B1C
为三棱柱ABC-A1B1C
![]() =3
=3


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |
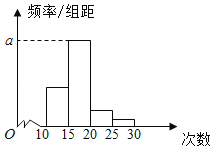
(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张三同学从7岁起到13岁每年生日时对自己的身高测量后记录如表:
年龄 (岁) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
身高 (cm) | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
(Ⅰ)求身高y关于年龄x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的线性回归方程,分析张三同学7岁至13岁身高的变化情况,如17岁之前都符合这一变化,请预测张三同学15岁时的身高.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:![]() =
= 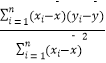 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别为双曲线
分别为双曲线![]() 的左、右顶点,双曲线的实轴长为
的左、右顶点,双曲线的实轴长为![]() ,焦点到渐近线的距离为
,焦点到渐近线的距离为![]() .
.
(1)求双曲线的方程;
(2)已知直线![]() 与双曲线的右支交于
与双曲线的右支交于![]() 两点,且在双曲线的右支上存在点
两点,且在双曲线的右支上存在点![]() ,使
,使![]() ,求
,求![]() 的值及点
的值及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个关于圆锥曲线的命题中:
①设![]() 为两个定点,
为两个定点,![]() 为非零常数,若
为非零常数,若![]() ,则动点
,则动点![]() 的轨迹是双曲线;
的轨迹是双曲线;
②方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;
有相同的焦点;
④已知抛物线![]() ,以过焦点的一条弦
,以过焦点的一条弦![]() 为直径作圆,则此圆与准线相切,其中真命题为__________.(写出所有真命题的序号)
为直径作圆,则此圆与准线相切,其中真命题为__________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() .
.
(1)若函数f(x)在定义域内不单调,求实数a的取值范围;
(2)若函数f(x)在区间(0,1]内单调递增,求实数a的取值范围;
(3)若x1、x2∈R+ , 且x1≤x2 , 求证:(lnx1﹣lnx2)(x1+2x2)≤3(x1﹣x2).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com