
| ||
| 2 |
|
| 1 |
| 2 |
| |PF1| |
| |PF2| |
| |MF1| |
| |F2M| |
| m+c |
| c-m |
| x2 |
| a2 |
| y2 |
| b2 |
| c2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
| 2b2 |
| a |
| ||
| 2 |
| c |
| a |
| ||
| 2 |
|
|
| x2 |
| 4 |
| 1 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| |PF1| |
| |PF2| |
| |MF1| |
| |F2M| |
| m+c |
| c-m |
m+
| ||
|
| 4-|PF2| |
| |PF2| |
| ||
|
| 2 |
| |PF2| |
| ||
|
2(
| ||
|
| 3 |
2(
| ||
|
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |


 µ¼Ń§Č«³ĢĮ·““ÓÅѵĮ·ĻµĮŠ“š°ø
µ¼Ń§Č«³ĢĮ·““ÓÅѵĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ČēĶ¼£¬ŌŚÖ±½Ē×ų±źĻµxOyÖŠ£¬ŅŃÖŖĶÖŌ²C£ŗ
ČēĶ¼£¬ŌŚÖ±½Ē×ų±źĻµxOyÖŠ£¬ŅŃÖŖĶÖŌ²C£ŗ| y2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| PA |
| AB |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ¹ć¶«Ź”½ŅŃōŹŠ2007ÄźøßÖŠ±ĻŅµ°ąµŚŅ»“Īøßæ¼Ä£Äāæ¼ŹŌĢā(ĄķæĘ) ĢāŠĶ£ŗ044
ČēĶ¼£¬ŌŚÖ±½Ē×ų±źĻµxOyÖŠ£¬ŅŃÖŖĶÖŌ²![]() µÄĄėŠÄĀŹe£½
µÄĄėŠÄĀŹe£½![]() £¬×óÓŅĮ½øö½¹·Ö±šĪŖF1”¢F2£®¹żÓŅ½¹µćF2ĒŅÓėxÖį“¹Ö±µÄÖ±ĻßÓėĶÖŌ²CĻą½»M”¢NĮ½µć£¬ĒŅ|MN|£½1£®
£¬×óÓŅĮ½øö½¹·Ö±šĪŖF1”¢F2£®¹żÓŅ½¹µćF2ĒŅÓėxÖį“¹Ö±µÄÖ±ĻßÓėĶÖŌ²CĻą½»M”¢NĮ½µć£¬ĒŅ|MN|£½1£®

(¢ń)ĒóĶÖŌ²CµÄ·½³Ģ£»
(¢ņ)ÉčĶÖŌ²CµÄ×󶄵ćĪŖA£¬ĻĀ¶„µćĪŖB£¬¶ÆµćPĀś×ć![]() £¬(
£¬(![]() )ŹŌĒóµćPµÄ¹ģ¼£·½³Ģ£¬Ź¹µćB¹ŲÓŚøĆ¹ģ¼£µÄ¶Ō³ĘµćĀäŌŚĶÖŌ²CÉĻ.
)ŹŌĒóµćPµÄ¹ģ¼£·½³Ģ£¬Ź¹µćB¹ŲÓŚøĆ¹ģ¼£µÄ¶Ō³ĘµćĀäŌŚĶÖŌ²CÉĻ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ2012-2013ѧğ¹ć¶«Ź”Õ潶žÖŠøßČż£ØÉĻ£©µŚŅ»“ĪŌĀæ¼ŹżŃ§ŹŌ¾ķ£ØĄķæĘ£©£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
 +
+ =1£Øa£¾b£¾0£©µÄĄėŠÄĀŹe=
=1£Øa£¾b£¾0£©µÄĄėŠÄĀŹe= £¬×óÓŅĮ½øö½¹·Ö±šĪŖF1”¢F2£®¹żÓŅ½¹µćF2ĒŅÓėÖį“¹Ö±µÄ
£¬×óÓŅĮ½øö½¹·Ö±šĪŖF1”¢F2£®¹żÓŅ½¹µćF2ĒŅÓėÖį“¹Ö±µÄ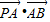 =m-4£¬£Øm”ŹR£©ŹŌĒóµćPµÄ¹ģ¼£·½³Ģ£¬Ź¹µćB¹ŲÓŚøĆ¹ģ¼£µÄ¶Ō³ĘµćĀäŌŚĶÖŌ²CÉĻ£®
=m-4£¬£Øm”ŹR£©ŹŌĒóµćPµÄ¹ģ¼£·½³Ģ£¬Ź¹µćB¹ŲÓŚøĆ¹ģ¼£µÄ¶Ō³ĘµćĀäŌŚĶÖŌ²CÉĻ£®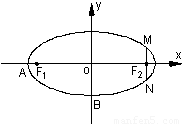
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ2010ğČĆɹųą·åŹŠøßČżĶ³æ¼ŹżŃ§ŹŌ¾ķ£ØĪÄæĘ£©£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
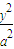 +
+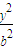 =1£Øa£¾b£¾0£©µÄĄėŠÄĀŹe=
=1£Øa£¾b£¾0£©µÄĄėŠÄĀŹe=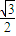 £¬×óÓŅĮ½øö½¹·Ö±šĪŖF1”¢F2£®¹żÓŅ½¹µćF2ĒŅÓėÖį“¹Ö±µÄ
£¬×óÓŅĮ½øö½¹·Ö±šĪŖF1”¢F2£®¹żÓŅ½¹µćF2ĒŅÓėÖį“¹Ö±µÄ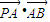 =m-4£¬£Øm”ŹR£©ŹŌĒóµćPµÄ¹ģ¼£·½³Ģ£¬Ź¹µćB¹ŲÓŚøĆ¹ģ¼£µÄ¶Ō³ĘµćĀäŌŚĶÖŌ²CÉĻ£®
=m-4£¬£Øm”ŹR£©ŹŌĒóµćPµÄ¹ģ¼£·½³Ģ£¬Ź¹µćB¹ŲÓŚøĆ¹ģ¼£µÄ¶Ō³ĘµćĀäŌŚĶÖŌ²CÉĻ£®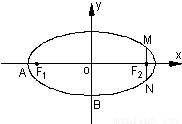
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com