
【题目】在直角坐标系xOy中,直线l的参数方程为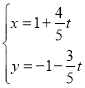 (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=cosθ﹣sinθ.
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=cosθ﹣sinθ.
(1)求直线l被曲线C所截得的弦长;
(2)若M(x,y)是曲线C上的动点,求x+y的最大值.
科目:高中数学 来源: 题型:
【题目】设![]() 是以
是以![]() 为焦点的抛物线
为焦点的抛物线![]() ,
,![]() 是以直线
是以直线![]() 与
与![]() 的渐近线,以
的渐近线,以![]() 为一个焦点的双曲线.
为一个焦点的双曲线.
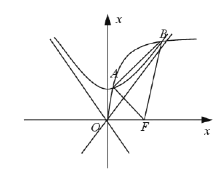
(1)求双曲线![]() 的标准方程;
的标准方程;
(2)若![]() 与
与![]() 在第一象限有两个公共点
在第一象限有两个公共点![]() ,求
,求![]() 的取值范围,并求
的取值范围,并求![]() 的最大值;
的最大值;
(3)是否存在正数![]() ,使得此时
,使得此时![]() 的重心
的重心![]() 恰好在双曲线
恰好在双曲线![]() 的渐近线上?如果存在,求出
的渐近线上?如果存在,求出![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车零件加工厂为迎接国庆大促销活动预估国庆七天销售量,该厂工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
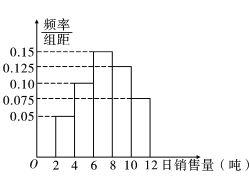
(1)根据频率分布直方图估计该厂的日平均销售量;(每组以中点值为代表)
(2)求未来![]() 天内,连续
天内,连续![]() 天日销售量不低于
天日销售量不低于![]() 吨,另一天日销售量低于
吨,另一天日销售量低于![]() 吨的概率;
吨的概率;
(3)用![]() 表示未来
表示未来![]() 天内日销售量不低于
天内日销售量不低于![]() 吨的天数,求随机变量
吨的天数,求随机变量![]() 的分布列、数学期望与方差.
的分布列、数学期望与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是________(写出所有正确命题的编号)
①命题“若![]() ,则
,则![]() 且
且![]() ”的否定是“若
”的否定是“若![]() ,则
,则![]() 且
且![]() ”
”
②已知函数![]() 的图象关于直线
的图象关于直线![]() 对称,函数
对称,函数![]() 为奇函数,则4是
为奇函数,则4是![]() 一个周期.
一个周期.
③平面![]() ,
,![]() ,过
,过![]() 内一点
内一点![]() 作
作![]() 的垂线
的垂线![]() ,则
,则![]() .
.
④在![]() 中角
中角![]() 所对的边分别为
所对的边分别为![]() ,若
,若![]() ,则
,则![]() 成等差数列.
成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
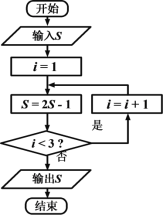
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax
(1)讨论函数f(x)的单调性;
(2)若存在x1<x2,且满足f(x1)=(x2).证明![]() ;
;
(3)证明:![]() (n∈N).
(n∈N).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD–A1B1C1D1中,已知底面ABCD是菱形,点P是侧棱C1C的中点.
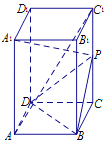
(1)求证:AC1∥平面PBD;
(2)求证:BD⊥A1P.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种抛硬币游戏的规则是:抛掷一枚硬币,每次正面向上得1分,反面向上得2分.
(1)设抛掷5次的得分为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)求恰好得到![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为![]()
![]() =
=![]() (
(![]() >0),过点
>0),过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线![]() 与曲线C相交于A,B两点.
与曲线C相交于A,B两点.
(Ⅰ)写出曲线C的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com