
【题目】已知四棱锥P﹣ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC= ![]() ,AB=1,M是PB的中点.
,AB=1,M是PB的中点. 
(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求面AMC与面BMC所成二面角的大小余弦值.
【答案】
(1)证明:∵PA⊥面ABCD,CD⊥AD,
∴由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD.
又CD面PCD,
∴面PAD⊥面PCD.
(2)解:过点B作BE∥CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连接AE,可知AC=CB=BE=AE= ![]() ,又AB=2,
,又AB=2,
所以四边形ACBE为正方形.由PA⊥面ABCD得∠PEB=90°
在Rt△PEB中BE=a2=3b2,PB= ![]() ,
,
∴cos∠PBE= ![]() .
.
∴AC与PB所成的角为arccos ![]() .
.
(3)解:作AN⊥CM,垂足为N,连接BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴△AMC≌△BMC,
∴BN⊥CM,故∠ANB为所求二面角的平面角
∵CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,ANMC= ![]() ,
,
∴AN= ![]() .
.
∴AB=2,
∴cos∠ANB= ![]() =﹣
=﹣ ![]()
故面AMC与面BMC所成二面角的大小余弦值为﹣ ![]() .
.
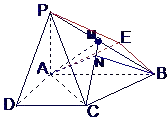
【解析】(1)证明面PAD⊥面PCD,只需证明面PCD内的直线CD,垂直平面PAD内的两条相交直线AD、PD即可;(2)过点B作BE∥CA,且BE=CA,∠PBE是AC与PB所成的角,解直角三角形PEB求AC与PB所成的角;(3)作AN⊥CM,垂足为N,连接BN,说明∠ANB为所求二面角的平面角,在三角形AMC中,用余弦定理求面AMC与面BMC所成二面角的大小.
【考点精析】关于本题考查的平面与平面垂直的判定和空间角的异面直线所成的角,需要了解一个平面过另一个平面的垂线,则这两个平面垂直;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则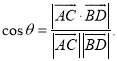 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(a,0)(a>0),B(0,a),C(﹣4,0),D(0,4)设△AOB的外接圆圆心为E. 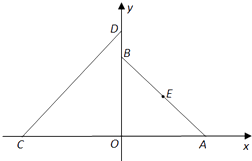
(1)若⊙E与直线CD相切,求实数a的值;
(2)设点P在圆E上,使△PCD的面积等于12的点P有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(Ⅰ)记线段![]() 的中点为
的中点为![]() ,在平面
,在平面![]() 内过点
内过点![]() 作一条直线与平面
作一条直线与平面![]() 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+)(ω>0,0≤≤π)为偶函数,其图象上相邻的两个最高点之间的距离为2π. (Ⅰ)求f(x)的解析式;
(Ⅱ)若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线m被两平行线l1:x+y=0与l2:x+y+ ![]() =0所截得的线段的长为2
=0所截得的线段的长为2 ![]() ,则m的倾斜角可以是
,则m的倾斜角可以是
①15° ②45° ③60° ④105°⑤120° ⑥165°
其中正确答案的序号是 . (写出所有正确答案的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是焦距为
分别是焦距为![]() 的椭圆
的椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为椭圆
为椭圆![]() 上非顶点的点,直
上非顶点的点,直![]() 线的斜率分别为
线的斜率分别为![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() (与
(与![]() 轴不重合)过点
轴不重合)过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 交于点
交于点![]() ,试求
,试求![]() 点的轨迹是否是垂直
点的轨迹是否是垂直![]() 轴的直线,若是,则求出
轴的直线,若是,则求出![]() 点的轨迹方程,若不是,请说明理由.
点的轨迹方程,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某金匠以黄金为原材料加工一种饰品,经多年的数据统计得知,该金匠平均每加5 个饰品中有4个成品和1个废品,每个成品可获利3万元,每个废品损失1万元,假设该金匠加工每件饰品互不影响,以频率估计概率.
(1)若金金匠加工4个饰品,求其中废品的数量不超过1的概率;
(2)若该金匠加工了 3个饰品,求他所获利润的数学期望.
(两小问的计算结果都用分数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com