
【题目】过点![]() 作圆
作圆![]() 的切线
的切线![]() ,已知
,已知![]() ,
,![]() 分别为切点,直线
分别为切点,直线![]() 恰好经过椭圆的右焦点和下顶点,则直线
恰好经过椭圆的右焦点和下顶点,则直线![]() 方程为___________;椭圆的标准方程是__________.
方程为___________;椭圆的标准方程是__________.
【答案】![]()
![]()
【解析】
①当过点![]() 的直线
的直线![]() 斜率不存在时,直线方程为
斜率不存在时,直线方程为![]() ,切点的坐标
,切点的坐标![]() ;
;
②当直线![]() 斜率存在时,设
斜率存在时,设![]() 方程为
方程为![]() ,根据圆心
,根据圆心![]() 到切线的距离等于半径
到切线的距离等于半径![]() ,求出
,求出![]() 确定直线方程,直线
确定直线方程,直线![]() 方程与圆方程的联立,进一步求出切点的坐标
方程与圆方程的联立,进一步求出切点的坐标![]() ,再求出
,再求出![]() 方程,则椭圆的右焦点及下顶点可求,其标准方程可求.
方程,则椭圆的右焦点及下顶点可求,其标准方程可求.
解:①当过点![]() 的直线
的直线![]() 斜率不存在时,直线方程为
斜率不存在时,直线方程为![]() ,切点的坐标
,切点的坐标![]() ;
;
②当直线![]() 斜率存在时,设
斜率存在时,设![]() 方程为
方程为![]() ,即
,即![]() ,
,
根据直线与圆相切,圆心![]() 到切线的距离等于半径
到切线的距离等于半径![]() ,得
,得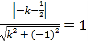
可以得到切线斜率![]() ,即
,即![]()
直线![]() 方程与圆方程的联立
方程与圆方程的联立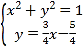
可以得切点的坐标![]() ,
,
根据![]() 、
、![]() 两点坐标可以得到直线
两点坐标可以得到直线![]() 方程为
方程为![]() ,(或利用过圆
,(或利用过圆![]() 上一点
上一点![]() 作圆的两条切线,则过两切点的直线方程为
作圆的两条切线,则过两切点的直线方程为![]() )
)
依题意,![]() 与
与![]() 轴的交点
轴的交点![]() 即为椭圆右焦点,得
即为椭圆右焦点,得![]() ,
,
与![]() 轴的交点
轴的交点![]() 即为椭圆下顶点坐标,所以
即为椭圆下顶点坐标,所以![]() ,
,
根据公式得![]() ,
,
因此,椭圆方程为![]() .
.


科目:高中数学 来源: 题型:
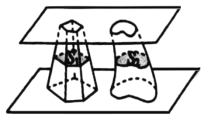
【题目】南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”.其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等,如图,夹在两个平行平面之间的两个几何体的体积分别为![]() ,
,![]() ,被平行于这两个平面的任意平面截得的两个截面面积分别为
,被平行于这两个平面的任意平面截得的两个截面面积分别为![]() 、
、![]() ,则“
,则“![]() 、
、![]() 不总相等”是“
不总相等”是“![]() ,
,![]() 不相等”的( )
不相等”的( )
A.充分而不必要条件B.必要而不充分条件
C.充分必要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设![]() ,用
,用![]() 表示不超过
表示不超过![]() 的最大整数,则
的最大整数,则![]() 称为高斯函数,例如:
称为高斯函数,例如:![]() ,
,![]() .已知函数
.已知函数![]() ,函数
,函数![]() ,则下列命题中真命题的个数是( )
,则下列命题中真命题的个数是( )
①![]() 图象关于
图象关于![]() 对称;
对称;
②![]() 是奇函数;
是奇函数;
③![]() 在
在![]() 上是增函数;
上是增函数;
④![]() 的值域是
的值域是![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某两名高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到折线图,下面是关于这两位同学的数学成绩分析.
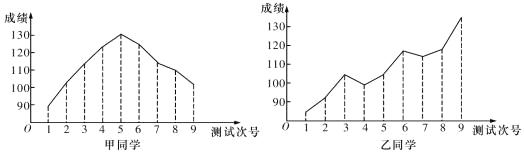
①甲同学的成绩折线图具有较好的对称性,故平均成绩为130分;
②根据甲同学成绩折线图提供的数据进行统计,估计该同学平均成绩在区间![]() 内;
内;
③乙同学的数学成绩与测试次号具有比较明显的线性相关性,且为正相关;
④乙同学连续九次测验成绩每一次均有明显进步.
其中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过点
的焦距为2,过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆的右焦点为F,定点![]() ,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线
,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线![]() 的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F1、F2分别为双曲线C:![]() (a>0,b>0)的左、右焦点,点M(x0,y0)(x0<0)为C的渐近线与圆x2+y2=a2的一个交点,O为坐标原点,若直线F1M与C的右支交于点N,且|MN|=|NF2|+|OF2|,则双曲线C的离心率为_____.
(a>0,b>0)的左、右焦点,点M(x0,y0)(x0<0)为C的渐近线与圆x2+y2=a2的一个交点,O为坐标原点,若直线F1M与C的右支交于点N,且|MN|=|NF2|+|OF2|,则双曲线C的离心率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com