
【题目】已知函数![]() ,
,![]() ,且函数
,且函数![]() 是偶函数.
是偶函数.
(1)求![]() 的解析式;
的解析式;
(2)若不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(3)若函数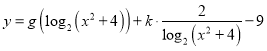 恰好有三个零点,求
恰好有三个零点,求![]() 的值及该函数的零点.
的值及该函数的零点.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】某地区工会利用 “健步行APP”开展健步走积分奖励活动.会员每天走5千步可获积分30分(不足5千步不积分),每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了1000名会员,统计了当天他们的步数,并将样本数据分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 九组,整理得到如下频率分布直方图:
九组,整理得到如下频率分布直方图:
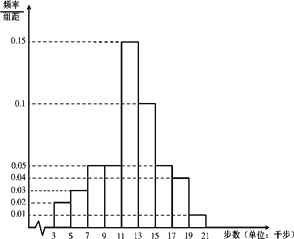
(Ⅰ)求当天这1000名会员中步数少于11千步的人数;
(Ⅱ)从当天步数在![]() ,
, ![]() ,
, ![]() 的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
(Ⅲ)写出该组数据的中位数(只写结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某小区为美化环境,建设美丽家园,计划在一块半径为R(R为常数)的扇形区域上,建个矩形的花坛CDEF和一个三角形的水池FCG.其中![]() ,O为圆心,
,O为圆心,![]() ,C,G,F在扇形圆弧上,D,E分别在半径OA,OB上,记OG与CF,DE分别交于M,N,
,C,G,F在扇形圆弧上,D,E分别在半径OA,OB上,记OG与CF,DE分别交于M,N,![]() .
.
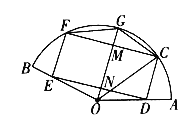
(1)求△FCG的面积S关于![]() 的关系式,并写出定义域;
的关系式,并写出定义域;
(2)若R=10米,花坛每平方米的造价是300元,试问矩形花坛的最高造价是多少?(取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动直![]() :x+my-2m=0与动直线
:x+my-2m=0与动直线![]() :mx-y-4m+2=0相交于点M,记动点M的轨迹为曲线C.
:mx-y-4m+2=0相交于点M,记动点M的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点P(-1,0)作曲线C的两条切线,切点分别为A,B,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=nan+n,数列{bn}的前n项和为Tn,求满足不等式![]() 的n的最小值.
的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题16分)某乡镇为了进行美丽乡村建设,规划在长为10千米的河流OC的一侧建一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数![]() ,
,![]() (单位:千米)的图象,且曲线段的顶点为
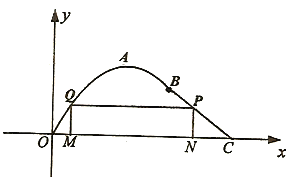
(单位:千米)的图象,且曲线段的顶点为![]() ;观光带的后一部分为线段BC,如图所示.
;观光带的后一部分为线段BC,如图所示.
(1)求曲线段OABC对应的函数![]() 的解析式;
的解析式;
(2)若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ,绿化带由线段MQ,QP, PN构成,其中点P在线段BC上.当OM长为多少时,绿化带的总长度最长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com