
【题目】如图为一简单组合体,其底面ABCD为正方形,棱PD与EC均垂直于底面ABCD,PD=2EC,N为PB的中点,求证: 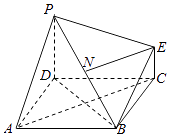
(1)平面EBC∥平面PDA;
(2)NE⊥平面PDB.
【答案】
(1)证明:∵PD⊥平面ABCD,CE⊥平面ABCD,∴EC∥PD,
又PD平面PDA,EC平面PDA,
∴EC∥平面PDA,
∵四边形ABCD为正方形,
∴BC∥AD,又AD平面PDA,BC平面PDA,
∴BC∥平面PDA,
∵EC平面EBC,BC平面EBC,EC∩BC=C,
∴平面EBC∥平面PDA
(2)证明:设AC与BD相交于点O,连接NO,
∵四边形ABCD为正方形,∴O为BD的中点,又N为PB的中点,
∴NO∥PD且NO= ![]() PD,
PD,
又由(1)得EC∥PD,且 ![]() ,
,
∴NO∥EC且NO=EC,∴四边形NOCE为平行四边形,
∴NE∥OC,即NE∥A,C
∵PD⊥平面ABCD,AC平面ABCD,∴AC⊥PD,
又DB⊥AC,PD∩BD=D
∴AC⊥平面PBD,又NE∥AC,
∴NE⊥平面PDB.
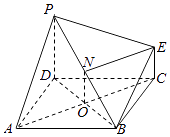
【解析】(1)由线面垂直性质得EC∥PD,由四边形ABCD为正方形,得BC∥AD,由此能证明平面EBC∥平面PDA.(2)推导出四边形NOCE为平行四边形,从而AC⊥PD,再由DB⊥AC,能证明NE⊥平面PDB.
【考点精析】本题主要考查了平面与平面平行的判定和直线与平面垂直的判定的相关知识点,需要掌握判断两平面平行的方法有三种:用定义;判定定理;垂直于同一条直线的两个平面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知正三棱锥P﹣ABC的底面边长为4,侧棱长为8,E,F分别为PB,PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P﹣AEF的体积. 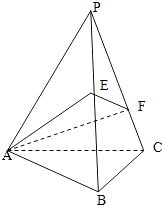
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正三棱柱ABC﹣A1B1C1的棱长都为2,E,F,G为 AB,AA1 , A1C1的中点,则B1F 与面GEF成角的正弦值( )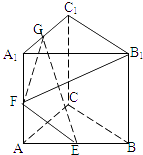
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D为AC的中点,∠ABC=90°,AA1=AB=2,BC=3. 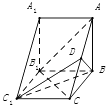
(1)求证:AB1∥平面BC1D;
(2)求三棱锥D﹣BC1C的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sin
sin ![]() ,1),
,1), ![]() =(cos
=(cos ![]() ,cos2
,cos2 ![]() ).
).
(Ⅰ)若 ![]()
![]() =1,求cos(
=1,求cos( ![]() ﹣x)的值;
﹣x)的值;
(Ⅱ)记f(x)= ![]()
![]() ,在△ABC中,A、B、C的对边分别为a、b、c,且满足(2a﹣c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,A、B、C的对边分别为a、b、c,且满足(2a﹣c)cosB=bcosC,求函数f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验。甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在![]() 区间内(满分100分),并绘制频率分布直方图如右图,两个班人数均为60人,成绩80分及以上为优良。
区间内(满分100分),并绘制频率分布直方图如右图,两个班人数均为60人,成绩80分及以上为优良。

根据以上信息填好下列![]() 联表,并判断出有多大的把握认为学生成绩优良与班级有关?
联表,并判断出有多大的把握认为学生成绩优良与班级有关?

(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选3人来作书面发言,求发言人至少有2人来自甲班的概率。
(以下临界值及公式仅供参考

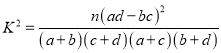 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点为
的左右焦点为![]() ,其离心率为
,其离心率为![]() ,又抛物线
,又抛物线![]() 在点
在点![]() 处的切线恰好过椭圆
处的切线恰好过椭圆![]() 的一个焦点.
的一个焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 斜率为
斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 的斜率分别为
的斜率分别为![]() ,是否存在常数
,是否存在常数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() (x≠0,a>0)是奇函数,且当x>0时,f(x)有最小值2
(x≠0,a>0)是奇函数,且当x>0时,f(x)有最小值2 ![]() .
.
(1)求f(x)的表达式;
(2)设数列{an}满足a1=2,2an+1=f(an)﹣an(n∈N*).令bn= ![]() ,求证bn+1=bn2;
,求证bn+1=bn2;
(3)求数列{bn}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com