
【题目】选修4-5:不等式选讲
已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若函数![]() 的值域为
的值域为![]() ,且
,且![]() ,求
,求![]() 的取值范围
的取值范围
科目:高中数学 来源: 题型:
【题目】为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h).试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(2)根据两组数据绘制茎叶图,从茎叶图看,哪种药的疗效更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,即
,即![]() ,若
,若![]() ,则称
,则称![]() 在
在![]() 上封闭.
上封闭.
(1)分别判断函数![]() ,
, ![]() 在
在![]() 上是否封闭,说明理由;
上是否封闭,说明理由;
(2)函数![]() 的定义域为
的定义域为![]() ,且存在反函数
,且存在反函数![]() ,若函数
,若函数![]() 在
在![]() 上封闭,且函数
上封闭,且函数![]() 在
在![]() 上也封闭,求实数
上也封闭,求实数![]() 的取值范围;
的取值范围;
(3)已知函数![]() 的定义域为
的定义域为![]() ,对任意
,对任意![]() ,若
,若![]() ,有
,有![]() 恒成立,则称
恒成立,则称![]() 在
在![]() 上是单射,已知函数
上是单射,已知函数![]() 在
在![]() 上封闭且单射,并且满足
上封闭且单射,并且满足![]()
![]() ,其中
,其中![]() (
(![]() ),
),![]() ,证明:存在
,证明:存在![]() 的真子集,
的真子集, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,使得
,使得![]() 在所有
在所有![]() (
(![]() )上封闭.
)上封闭.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国“雾霾天气”频发,严重影响人们的身体健康.根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
API | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 | 251~300 | >300 |
级别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
状况 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
|
|
|
|
| |||
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图.
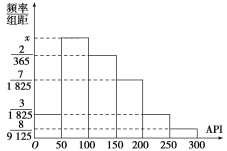
(1)求频率分布直方图中x的值;
(2)计算一年中空气质量分别为良和轻微污染的天数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子里有编号为![]() 的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲又说:“我可以确定了.”
根据以上信息, 你可以推断出抽取的两球中
A. 一定有3号球 B. 一定没有3号球 C. 可能有5号球 D. 可能有6号球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com