
【题目】设![]() ,
,![]() 是
是![]() 的两个非空子集,如果存在一个函数
的两个非空子集,如果存在一个函数![]() 满足:①
满足:① ![]() ;② 对任意
;② 对任意![]() ,当
,当![]() 时,恒有
时,恒有![]() ,那么称这两个集合为“
,那么称这两个集合为“![]() 到
到![]() 的保序同构”,以下集合对不是“
的保序同构”,以下集合对不是“![]() 到
到![]() 的保序同构”的是( )
的保序同构”的是( )
A.![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为R,且对于任意x∈R,都有
的定义域为R,且对于任意x∈R,都有![]() 及
及![]() 成立,当
成立,当![]() 且
且![]() 时,都有
时,都有![]() 成立,下列四个结论中不正确命题是( )
成立,下列四个结论中不正确命题是( )
A.![]() B.函数
B.函数![]() 在区间
在区间![]() 上为增函数
上为增函数
C.直线![]() 是函数
是函数![]() 的一条对称轴D.方程
的一条对称轴D.方程![]() 在区间
在区间![]() 上有4个不同的实根
上有4个不同的实根
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=![]() PD,则平面PQC与平面DCQ的位置关系为( )
PD,则平面PQC与平面DCQ的位置关系为( )

A. 平行 B. 垂直
C. 相交但不垂直 D. 位置关系不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:x2+y2=1与圆C2:x2+y2﹣6x+m=0.
(1)若圆C1与圆C2外切,求实数m的值;
(2)在(1)的条件下,若直线x+2y+n=0与圆C2的相交弦长为2![]() ,求实数n的值.
,求实数n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点作直线交抛物线于
的焦点作直线交抛物线于![]() ,
,![]() 两点,若
两点,若![]() ,则
,则![]() 的值为( )
的值为( )
A. 10 B. 8 C. 6 D. 4
【答案】B
【解析】
根据过抛物线焦点的弦长公式,利用题目所给已知条件,求得弦长![]() .
.
根据过抛物线焦点的弦长公式有![]() .故选B.
.故选B.
【点睛】
本小题主要考查过抛物线焦点的弦长公式,即![]() .要注意只有过抛物线焦点的弦长才可以使用.属于基础题.
.要注意只有过抛物线焦点的弦长才可以使用.属于基础题.
【题型】单选题
【结束】
10
【题目】已知椭圆![]() :
: ![]() 的右顶点、上顶点分别为
的右顶点、上顶点分别为![]() 、
、![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,则椭圆
,则椭圆![]() 的方程为( )
的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品![]() 的直径均位于区间
的直径均位于区间![]() 内(单位:
内(单位: ![]() ).若生产一件产品
).若生产一件产品![]() 的直径位于区间
的直径位于区间![]() 内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品
内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品![]() 中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
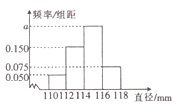
(1)求![]() 的值,并估计该厂生产一件
的值,并估计该厂生产一件![]() 产品的平均利润;
产品的平均利润;
(2)现用分层抽样法从直径位于区间![]() 内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间
内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间![]() 内的槪率.
内的槪率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象关于直线
,其图象关于直线![]() 对称,为了得到函数
对称,为了得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上的所有点( )
的图象上的所有点( )
A.先向左平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
B.先向右平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
C.先向右平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
D.先向左平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com