
分析 (1)捆绑法:把3名女生看作1个元素与其它排列,由分步计数原理可得;
(2)插空法:先排4名男生,在把3名女生插到所产生的5个空位,由分步计数原理可得;
(3)将排法分成两类,一类是甲站在排尾,其余的可全排,有$A_6^6$种排法;另一类是甲既不站排尾又不站排头,有$A_5^1$种排法,乙不站排尾而站余下的5个位置中一个,有$A_5^1$种排法,其余人全排列.
解答 解:(1)女生必须站在一起,是女生的全排列,有$A_3^3$种排法.全体女生视为一个元素与其他男生全排列有$A_5^5$种排法.由分步乘法计数原理知,共有$A_3^3•A_5^5=720$(种);
(2)分两步,第一步:男生的全排列有$A_4^4$种排法;第二步:男生排好后,男生之间有3个空,加上男生排列的两端共5个空,女生在这5个空中排列,有$A_5^3$种排法,由分步乘法计数原理知,共有$A_4^4•A_5^3=1440$(种);
(3)将排法分成两类,一类是甲站在排尾,其余的可全排,有$A_6^6$种排法;另一类是甲既不站排尾又不站排头,有$A_5^1$种排法,乙不站排尾而站余下的5个位置中一个,有$A_5^1$种排法,其余人全排列,于是这一类有$A_5^1•A_5^1•A_5^{51}$种排法,有分类加法计数原理知,共有$A_6^6$+$A_5^1•A_5^1•A_5^5$=3720(种)
点评 本题考查排列组合及简单的计数问题,涉及间接法和捆绑,插空等方法的应用,属中档题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
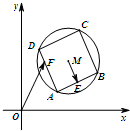 如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8.
如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com