Question

已知点P(x,y)是圆(x+2)²+y²=1上任意一点.

(1)求P点到直线3x+4y+12=0的距离的最大值和最小值;

(2)求x-2y的最大值和最小值;

(3)求的最大值和最小值.

Answer 1

解析：(1)&(3)题中的目标函数均有两个变量x、y,因此可通过圆的参数方程化为一个变量的函数,再求最值.?

运用数形结合的思想求解.第(1)题中,设圆心到直线的距离为d,则由图可知,最大值为d+r,最小值为d-r.第(2)题中设t=x-2y,则当直线与圆相切时,t分别取得最大值和最小值.第(3)题中,将看成图上一点P(x,y)与定点(1,2)连线的斜率,因此当直线y-2=k(x-1)与圆相切时取得最值.

解法一:圆的参数方程为(θ为参数).

∵P(x,y)在圆上,?

∴可设

(1)点P到直线3x+4y+12=0的距离为

∵|sin(θ-β)|≤1,

解法二:(1)圆心C(-2,0)到直线3x+4y+12=0的距离为

∴P点到直线3x+4y+12=0的距离的最大值为d+r=

(2)设t=x-2y,则直线x-2y-t=0与圆(x-2)²+y²=1有公共点.?

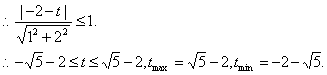
(3)设则直线kx-y-k+2=0与圆(x-2)²+y²=1有公共点,