
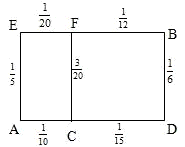
 张先生居住在城镇的A处,准备开车到单位B处上班.若该城镇各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次.已知发生堵车事件的概率如图所示(例如A→C→D算作两个路段:路段A→C发生堵车事件的概率是
张先生居住在城镇的A处,准备开车到单位B处上班.若该城镇各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次.已知发生堵车事件的概率如图所示(例如A→C→D算作两个路段:路段A→C发生堵车事件的概率是 ,路段C→D发生堵车事件的概率是
,路段C→D发生堵车事件的概率是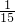 ).
).
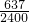
 ,
,


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:
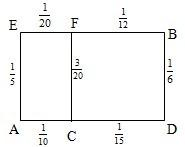 张先生居住在城镇的A处,准备开车到单位B处上班.若该城镇各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次.已知发生堵车事件的概率如图所示(例如A→C→D算作两个路段:路段A→C发生堵车事件的概率是
张先生居住在城镇的A处,准备开车到单位B处上班.若该城镇各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次.已知发生堵车事件的概率如图所示(例如A→C→D算作两个路段:路段A→C发生堵车事件的概率是| 1 |
| 10 |
| 1 |
| 15 |
查看答案和解析>>
科目:高中数学 来源:2011年四川省宜宾市高考数学调研试卷(文科)(解析版) 题型:解答题
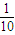 ,路段C→D发生堵车事件的概率是
,路段C→D发生堵车事件的概率是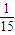 ).
).
查看答案和解析>>
科目:高中数学 来源:2011年四川省宜宾市高考数学调研试卷(理科)(解析版) 题型:解答题
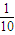 ,路段C→D发生堵车事件的概率是
,路段C→D发生堵车事件的概率是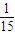 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com